Microseismic Monitoring and Geomechanical Modelling of CO2 - bris

CHAPTER 4. A COMPARISON OF MICROSEISMIC MONITORING OF FRACTURE STIMULATION DUE TO WATER
VERSUS CO 2 INJECTION
0.2
0.0
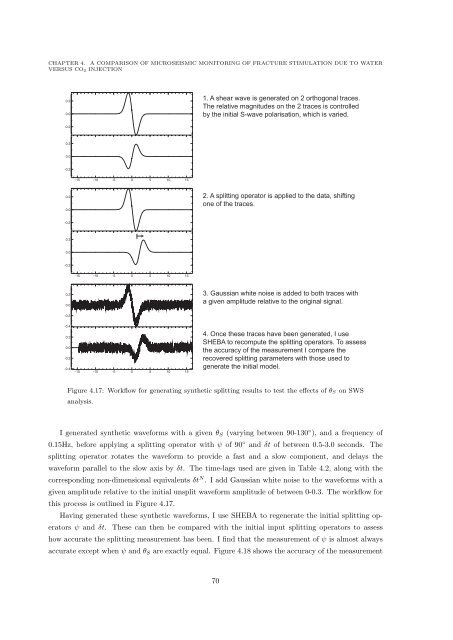
1. A shear wave is generated on 2 orthogonal traces.
The relative magnitudes on the 2 traces is controlled
by the initial S-wave polarisation, which is varied.
-0.2
0.2
0.0
-0.2
-15 -10 -5 0 5 10 15
0.2
0.0
2. A splitting operator is applied to the data, shifting
one of the traces.
-0.2
0.2
0.0
-0.2
-15 -10 -5 0 5 10 15
0.2
0.0
3. Gaussian white noise is added to both traces with
a given amplitude relative to the original signal.
-0.2
-0.4
0.2
0.0
-0.2
-0.4
-15 -10 -5 0 5 10 15
4. Once these traces have been generated, I use
SHEBA to recompute the splitting operators. To assess
the accuracy of the measurement I compare the
recovered splitting parameters with those used to
generate the initial model.
Figure 4.17: Workflow for generating synthetic splitting results to test the effects of θ S on SWS
analysis.
I generated synthetic waveforms with a given θ S (varying between 90-130 ◦ ), and a frequency of
0.15Hz, before applying a splitting operator with ψ of 90 ◦ and δt of between 0.5-3.0 seconds. The
splitting operator rotates the waveform to provide a fast and a slow component, and delays the
waveform parallel to the slow axis by δt. The time-lags used are given in Table 4.2, along with the
corresponding non-dimensional equivalents δt N . I add Gaussian white noise to the waveforms with a
given amplitude relative to the initial unsplit waveform amplitude of between 0-0.3. The workflow for
this process is outlined in Figure 4.17.
Having generated these synthetic waveforms, I use SHEBA to regenerate the initial splitting operators
ψ and δt. These can then be compared with the initial input splitting operators to assess
how accurate the splitting measurement has been. I find that the measurement of ψ is almost always
accurate except when ψ and θ S are exactly equal. Figure 4.18 shows the accuracy of the measurement
70