Nichtlineare Methoden zur Quantifizierung von Abhängigkeiten und ...

64 KAPITEL 4. EXKURS: DYNAMISCHE SYSTEME
..
..
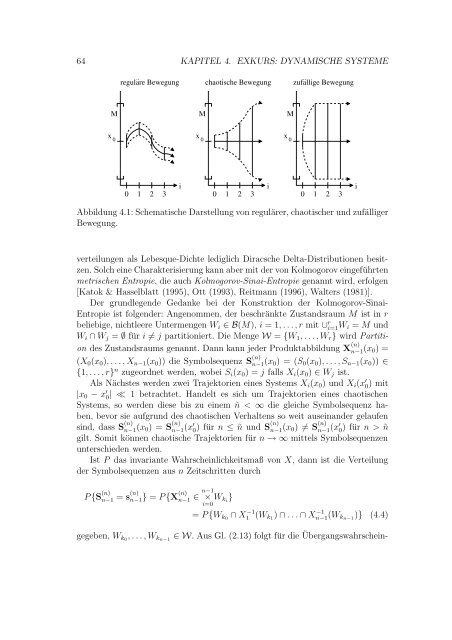
regulare Bewegung chaotische Bewegung zufallige Bewegung
M
M
M
x
0
x 0
x 0
i
i
0 1 2 3 0 1 2 3 0 1 2
3
i
Abbildung 4.1: Schematische Darstellung von regulärer, chaotischer und zufälliger
Bewegung.
verteilungen als Lebesque-Dichte lediglich Diracsche Delta-Distributionen besitzen.
Solch eine Charakterisierung kann aber mit der von Kolmogorov eingeführten
metrischen Entropie, die auch Kolmogorov-Sinai-Entropie genannt wird, erfolgen
[Katok & Hasselblatt (1995), Ott (1993), Reitmann (1996), Walters (1981)].
Der grundlegende Gedanke bei der Konstruktion der Kolmogorov-Sinai-
Entropie ist folgender: Angenommen, der beschränkte Zustandsraum M ist in r
beliebige, nichtleere Untermengen W i ∈ B(M), i = 1, . . . , r mit ∪ r i=1 W i = M und
W i ∩ W j = ∅ für i ≠ j partitioniert. Die Menge W = {W 1 , . . . , W r } wird Partition
des Zustandsraums genannt. Dann kann jeder Produktabbildung X (n)
n−1 (x 0) =
(X 0 (x 0 ), . . . , X n−1 (x 0 )) die Symbolsequenz S (n)
n−1(x 0 ) = (S 0 (x 0 ), . . . , S n−1 (x 0 )) ∈
{1, . . . , r} n zugeordnet werden, wobei S i (x 0 ) = j falls X i (x 0 ) ∈ W j ist.
Als Nächstes werden zwei Trajektorien eines Systems X i (x 0 ) und X i (x ′ 0) mit
|x 0 − x ′ 0 | ≪ 1 betrachtet. Handelt es sich um Trajektorien eines chaotischen
Systems, so werden diese bis zu einem ñ < ∞ die gleiche Symbolsequenz haben,
bevor sie aufgrund des chaotischen Verhaltens so weit auseinander gelaufen
sind, dass S (n)
n−1 (x 0) = S (n)
n−1 (x′ 0 ) für n ≤ ñ und S(n) n−1 (x 0) ≠ S (n)
n−1 (x′ 0 ) für n > ñ
gilt. Somit können chaotische Trajektorien für n → ∞ mittels Symbolsequenzen
unterschieden werden.
Ist P das invariante Wahrscheinlichkeitsmaß von X, dann ist die Verteilung
der Symbolsequenzen aus n Zeitschritten durch
P {S (n)
n−1 = s (n)
n−1} = P {X (n)
n−1 ∈ n−1
×
i=0
W ki }
= P {W k0 ∩ X −1
1 (W k 1
) ∩ . . . ∩ X −1
n−1 (W k n−1
)} (4.4)
gegeben, W k0 , . . . , W kn−1 ∈ W. Aus Gl. (2.13) folgt für die Übergangswahrschein-