cours et TD - Enseeiht

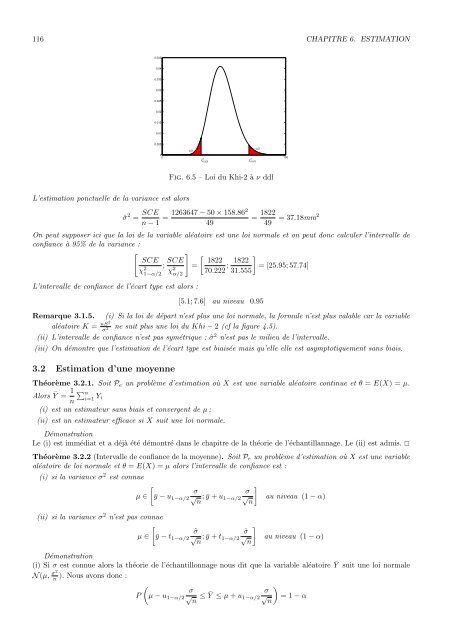
116 CHAPITRE 6. ESTIMATION0.0450.040.0350.030.0250.020.0150.010.005α/2→← α/200 10022χ 0.025χ 0.975Fig. 6.5 – Loi du Khi-2 à ν ddlL’estimation ponctuelle de la variance est alorsˆσ 2 = SCE 1263647 − 50 × 158.862= = 1822n − 1 4949 = 37.18mm2On peut supposer ici que la loi de la variable aléatoire est une loi normale et on peut donc calculer l’intervalle deconfiance à 95% de la variance :[]SCEχ 2 ; SCE [ ]18221−α/2χ 2 =α/270.222 ; 1822= [25.95; 57.74]31.555L’intervalle de confiance de l’écart type est alors :[5.1; 7.6] au niveau 0.95Remarque 3.1.5. (i) Si la loi de départ n’est plus une loi normale, la formule n’est plus valable car la variablealéatoire K = nS2σne suit plus une loi du Khi − 2 (cf la figure 4.5).2(ii) L’intervalle de confiance n’est pas symétrique : ˆσ 2 n’est pas le milieu de l’intervalle.(iii) On démontre que l’estimation de l’écart type est biaisée mais qu’elle elle est asymptotiquement sans biais.3.2 Estimation d’une moyenneThéorème 3.2.1. Soit P e un problème d’estimation où X est une variable aléatoire continue et θ = E(X) = µ.Alors Ȳ = 1 n∑ ni=1 Y i(i) est un estimateur sans biais et convergent de µ ;(ii) est un estimateur efficace si X suit une loi normale.DémonstrationLe (i) est immédiat et a déjà été démontré dans le chapitre de la théorie de l’échantillannage. Le (ii) est admis. ✷Théorème 3.2.2 (Intervalle de confiance de la moyenne). Soit P e un problème d’estimation où X est une variablealéatoire de loi normale et θ = E(X) = µ alors l’intervalle de confiance est :(i) si la variance σ 2 est connue]σ σµ ∈[ȳ − u 1−α/2 √n ; ȳ + u 1−α/2 √nau niveau (1 − α)(ii) si la variance σ 2 n’est pas connue]ˆσ ˆσµ ∈[ȳ − t 1−α/2 √n ; ȳ + t 1−α/2 √nau niveau (1 − α)Démonstration(i) Si σ est connue alors la théorie de l’échantillonnage nous dit que la variable aléatoire Ȳ suit une loi normaleN (µ, σ2n). Nous avons donc :()σP µ − u 1−α/2 √n ≤ Ȳ ≤ µ + u σ1−α/2 √ = 1 − αn