cours et TD - Enseeiht

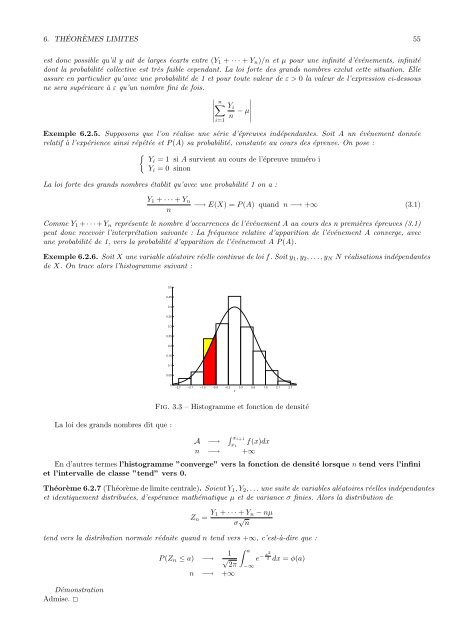
6.THÉORÈMES LIMITES 55est donc possible qu’il y ait de larges écarts entre (Y 1 + · · · + Y n )/n et µ pour une infinité d’événements, infinitédont la probabilité collective est très faible cependant. La loi forte des grands nombres exclut cette situation. Elleassure en particulier qu’avec une probabilité de 1 et pour toute valeur de ε > 0 la valeur de l’expression ci-dessousne sera supérieure à ε qu’un nombre fini de fois.∣ n∑ Y ∣∣∣∣i∣ n − µi=1Exemple 6.2.5. Supposons que l’on réalise une série d’épreuves indépendantes. Soit A un événement donnéerelatif à l’expérience ainsi répétée et P (A) sa probabilité, constante au cours des épreuve. On pose :{Yi = 1 si A survient au cours de l’épreuve numéro iY i = 0 sinonLa loi forte des grands nombres établit qu’avec une probabilité 1 on a :Y 1 + · · · + Y nn−→ E(X) = P (A) quand n −→ +∞ (3.1)Comme Y 1 + · · · + Y n représente le nombre d’occurrences de l’événement A au cours des n premières épreuves (3.1)peut donc recevoir l’interprétation suivante : La fréquence relative d’apparition de l’événement A converge, avecune probabilité de 1, vers la probabilité d’apparition de l’événement A P (A).Exemple 6.2.6. Soit X une variable aléatoire réelle continue de loi f. Soit y 1 , y 2 , . . . , y N N réalisations indépendantesde X. On trace alors l’histogramme suivant :0.50.450.40.350.30.250.20.150.10.050−2.7 −2.1 −1.5 −0.9 −0.3 0.3 0.9 1.5 2.1 2.7xLa loi des grands nombres dit que :Fig. 3.3 – Histogramme et fonction de densitéA −→ ∫ x i+1x if(x)dxn −→ +∞En d’autres termes l’histogramme ”converge” vers la fonction de densité lorsque n tend vers l’infiniet l’intervalle de classe ”tend” vers 0.Théorème 6.2.7 (Théorème de limite centrale). Soient Y 1 , Y 2 , . . . une suite de variables aléatoires réelles indépendanteset identiquement distribuées, d’espérance mathématique µ et de variance σ finies. Alors la distribution deZ n = Y 1 + · · · + Y n − nµσ √ ntend vers la distribution normale réduite quand n tend vers +∞, c’est-à-dire que :DémonstrationAdmise. ✷P (Z n ≤ a) −→ 1 √2π∫ an −→ +∞−∞e − x22 dx = φ(a)