- Page 1 and 2: T.C. ANADOLU ÜN‹VERS‹TES‹ YA
- Page 3 and 4: İçindekileriiiİçindekiler1 Beli
- Page 6 and 7: GökçeZeynepMATEMATİK IISelçukEn
- Page 8 and 9: 2 1 Belirli ve Belirsiz İntegralG
- Page 11 and 12: 5Bölgeyi dıştan sınırlayan dik
- Page 13 and 14: Alan Hesaplamaları 7Babilliler ve
- Page 15 and 16: Alan Hesaplamaları 9Evet Zeynep, t
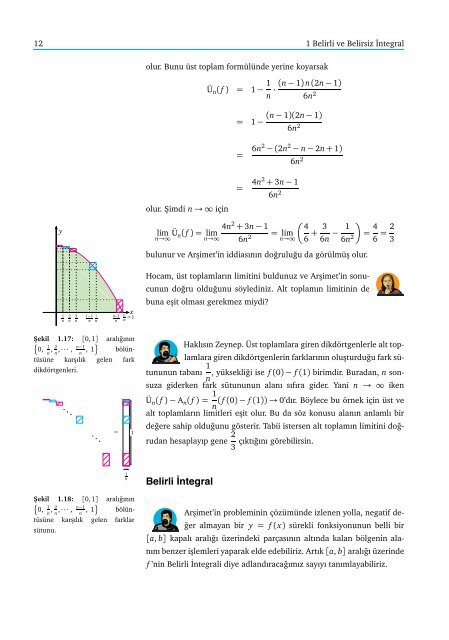
- Page 17: Alan Hesaplamaları 11Ü n (f)= f(0
- Page 21 and 22: Belirsiz İntegral 15Belirsiz İnte
- Page 24 and 25: 18 1 Belirli ve Belirsiz İntegral
- Page 26 and 27: 20 1 Belirli ve Belirsiz İntegral
- Page 28 and 29: 22 1 Belirli ve Belirsiz İntegralA
- Page 30 and 31: 24 1 Belirli ve Belirsiz İntegral
- Page 32 and 33: 26 1 Belirli ve Belirsiz İntegraly
- Page 34 and 35: 28 1 Belirli ve Belirsiz İntegralO
- Page 36 and 37: 30 1 Belirli ve Belirsiz İntegral
- Page 38 and 39: 32 2 Diferansiyel DenklemlerDiferan
- Page 40 and 41: 34 2 Diferansiyel DenklemlerTanım
- Page 42 and 43: 36 2 Diferansiyel DenklemlerHocam n
- Page 44 and 45: 38 2 Diferansiyel Denklemleryc 1 =
- Page 46 and 47: 40 2 Diferansiyel Denklemleryy= y 0
- Page 48 and 49: 42 2 Diferansiyel DenklemlerRadyoak
- Page 50 and 51: 44 2 Diferansiyel Denklemlere ş i
- Page 52 and 53: 46 2 Diferansiyel DenklemlerEvet En
- Page 54 and 55: 48 2 Diferansiyel DenklemlerHocam N
- Page 56 and 57: 50 2 Diferansiyel DenklemlerSınır
- Page 58 and 59: 52 2 Diferansiyel Denklemlerya da 7
- Page 60 and 61: 54 2 Diferansiyel Denklemlerolur. S
- Page 62 and 63: 56 2 Diferansiyel DenklemlerÇıkar
- Page 64 and 65: 58 2 Diferansiyel Denklemler9. Prob
- Page 66 and 67: 60 3 Doğrusal Programlamaya Giriş
- Page 68 and 69:
62 3 Doğrusal Programlamaya Giriş
- Page 70 and 71:
64 3 Doğrusal Programlamaya Giriş
- Page 72 and 73:
66 3 Doğrusal Programlamaya Giriş
- Page 74 and 75:
68 3 Doğrusal Programlamaya Giriş
- Page 76 and 77:
70 3 Doğrusal Programlamaya Giriş
- Page 78 and 79:
72 3 Doğrusal Programlamaya Giriş
- Page 80 and 81:
74 3 Doğrusal Programlamaya Giriş
- Page 82 and 83:
76 3 Doğrusal Programlamaya Giriş
- Page 84 and 85:
78 3 Doğrusal Programlamaya Giriş
- Page 86 and 87:
80 3 Doğrusal Programlamaya Giriş
- Page 88 and 89:
82 4 İktisadi UygulamalarTüketici
- Page 90 and 91:
84 4 İktisadi Uygulamalarformülü
- Page 92 and 93:
86 4 İktisadi Uygulamalar 0,5·203
- Page 94 and 95:
88 4 İktisadi Uygulamalar= 32− 8
- Page 96 and 97:
90 4 İktisadi UygulamalarKorkma Se
- Page 98 and 99:
92 4 İktisadi UygulamalarArkadaşl
- Page 100 and 101:
94 4 İktisadi UygulamalarGini inde
- Page 102 and 103:
96 4 İktisadi UygulamalarBunu ben
- Page 104 and 105:
98 4 İktisadi Uygulamalaredeceğiz
- Page 106 and 107:
100 4 İktisadi UygulamalarÇıkar
- Page 108 and 109:
102 4 İktisadi Uygulamalar6. Bu ü
- Page 110 and 111:
104 5 Çizge Kuramına GirişÇizge
- Page 112 and 113:
106 5 Çizge Kuramına Girişcdbeah
- Page 114 and 115:
108 5 Çizge Kuramına GirişBir ç
- Page 116 and 117:
110 5 Çizge Kuramına GirişTüm k
- Page 118 and 119:
112 5 Çizge Kuramına GirişAma ho
- Page 120 and 121:
114 5 Çizge Kuramına GirişŞöyl
- Page 122 and 123:
116 5 Çizge Kuramına GirişÇok g
- Page 124 and 125:
118 5 Çizge Kuramına GirişMete H
- Page 126 and 127:
120 5 Çizge Kuramına GirişBir ü
- Page 128 and 129:
122 5 Çizge Kuramına GirişÇizge
- Page 130 and 131:
124 5 Çizge Kuramına GirişAğaç
- Page 132 and 133:
126 5 Çizge Kuramına GirişEngin
- Page 134 and 135:
128 5 Çizge Kuramına GirişOkuma
- Page 136 and 137:
•••••••••••
- Page 138 and 139:
132 6 Asal Sayılar ve Modüler Ari
- Page 140 and 141:
134 6 Asal Sayılar ve Modüler Ari
- Page 142 and 143:
136 6 Asal Sayılar ve Modüler Ari
- Page 144 and 145:
138 6 Asal Sayılar ve Modüler Ari
- Page 146 and 147:
140 6 Asal Sayılar ve Modüler Ari
- Page 148 and 149:
142 6 Asal Sayılar ve Modüler Ari
- Page 150 and 151:
144 6 Asal Sayılar ve Modüler Ari
- Page 152 and 153:
146 6 Asal Sayılar ve Modüler Ari
- Page 154 and 155:
148 6 Asal Sayılar ve Modüler Ari
- Page 156 and 157:
150 6 Asal Sayılar ve Modüler Ari
- Page 158 and 159:
152 6 Asal Sayılar ve Modüler Ari
- Page 160 and 161:
154 6 Asal Sayılar ve Modüler Ari
- Page 162 and 163:
156 6 Asal Sayılar ve Modüler Ari
- Page 164 and 165:
158 7 Şifreleme Kuramına GirişG
- Page 166 and 167:
160 7 Şifreleme Kuramına GirişGe
- Page 168 and 169:
162 7 Şifreleme Kuramına GirişPe
- Page 170 and 171:
164 7 Şifreleme Kuramına GirişBu
- Page 172 and 173:
166 7 Şifreleme Kuramına Girişol
- Page 174 and 175:
168 7 Şifreleme Kuramına GirişEv
- Page 176 and 177:
170 7 Şifreleme Kuramına GirişDi
- Page 178 and 179:
172 7 Şifreleme Kuramına GirişHo
- Page 180 and 181:
174 7 Şifreleme Kuramına Girişp
- Page 182 and 183:
176 7 Şifreleme Kuramına GirişBu
- Page 184 and 185:
178 7 Şifreleme Kuramına GirişDe
- Page 186 and 187:
180 7 Şifreleme Kuramına GirişOk
- Page 188 and 189:
182 7 Şifreleme Kuramına GirişÇ
- Page 190 and 191:
184 8 Oyunlar Kuramına GirişG i r
- Page 192 and 193:
186 8 Oyunlar Kuramına GirişZeyne
- Page 194 and 195:
188 8 Oyunlar Kuramına GirişBu oy
- Page 196 and 197:
190 8 Oyunlar Kuramına GirişBu ö
- Page 198 and 199:
192 8 Oyunlar Kuramına GirişBu se
- Page 200 and 201:
194 8 Oyunlar Kuramına GirişMaksi
- Page 202 and 203:
196 8 Oyunlar Kuramına GirişDenge
- Page 204 and 205:
198 8 Oyunlar Kuramına GirişSıf
- Page 206 and 207:
200 8 Oyunlar Kuramına GirişOkuma
- Page 208 and 209:
202 8 Oyunlar Kuramına GirişÇöz
- Page 210 and 211:
204 KaynakçaŞekil 2.8: en.wikiped
- Page 212:
206 Dizinköşe noktası, 104kripta