Etude numérique de la fissuration d'un milieu viscoélastique - Pastel
Etude numérique de la fissuration d'un milieu viscoélastique - Pastel
Etude numérique de la fissuration d'un milieu viscoélastique - Pastel
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
Angle <strong>de</strong> phase δ (°)<br />
80<br />
70<br />
60<br />
50<br />
40<br />
30<br />
20<br />
10<br />
30 °C<br />
20 °C<br />
10 °C<br />
0 °C<br />
−10 °C<br />
−15 °C<br />
−20 °C<br />
0<br />
0 500 1000 1500 2000<br />
|E*| (MPa)<br />
(a) L’espace B<strong>la</strong>ck<br />
4.3. Caractérisation dans le domaine fréquentiel<br />
E’’ (MPa)<br />
300<br />
250<br />
200<br />
150<br />
100<br />
50<br />
30 °C<br />
20 °C<br />
10 °C<br />
0 °C<br />
−10 °C<br />
−15 °C<br />
−20 °C<br />
0<br />
0 500 1000 1500 2000<br />
E’ (MPa)<br />
(b) Le p<strong>la</strong>n Cole-Cole<br />
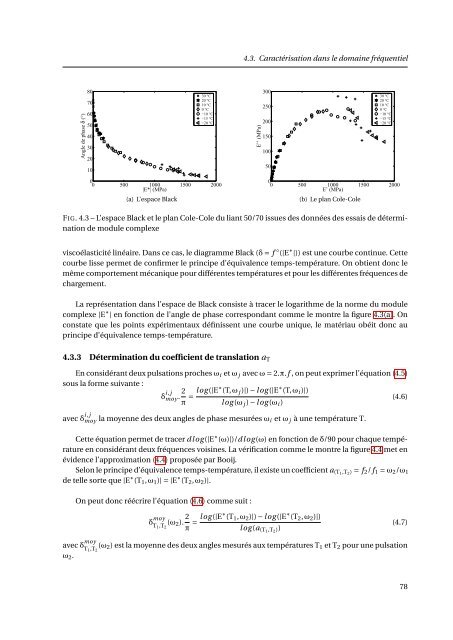
FIG. 4.3 – L’espace B<strong>la</strong>ck et le p<strong>la</strong>n Cole-Cole du liant 50/70 issues <strong>de</strong>s données <strong>de</strong>s essais <strong>de</strong> détermination<br />
<strong>de</strong> module complexe<br />
viscoé<strong>la</strong>sticité linéaire. Dans ce cas, le diagramme B<strong>la</strong>ck (δ = f ◦ (|E ∗ |)) est une courbe continue. Cette<br />
courbe lisse permet <strong>de</strong> confirmer le principe d’équivalence temps-température. On obtient donc le<br />
même comportement mécanique pour différentes températures et pour les différentes fréquences <strong>de</strong><br />
chargement.<br />
La représentation dans l’espace <strong>de</strong> B<strong>la</strong>ck consiste à tracer le logarithme <strong>de</strong> <strong>la</strong> norme du module<br />
complexe |E ∗ | en fonction <strong>de</strong> l’angle <strong>de</strong> phase correspondant comme le montre <strong>la</strong> figure 4.3(a). On<br />
constate que les points expérimentaux définissent une courbe unique, le matériau obéit donc au<br />
principe d’équivalence temps-température.<br />
4.3.3 Détermination du coefficient <strong>de</strong> trans<strong>la</strong>tion aT<br />
En considérant <strong>de</strong>ux pulsations proches ωi et ωj avec ω = 2.π.f , on peut exprimer l’équation (4.5)<br />
sous <strong>la</strong> forme suivante :<br />
i ,j<br />
δmoy . 2<br />
π = log (|E∗ (T,ωj )|) − log (|E∗ (T,ωi )|)<br />
log (ωj ) − log (ωi )<br />
(4.6)<br />
i ,j<br />
avec δmoy <strong>la</strong> moyenne <strong>de</strong>s <strong>de</strong>ux angles <strong>de</strong> phase mesurées ωi et ωj à une température T.<br />
Cette équation permet <strong>de</strong> tracer dl og (|E ∗ (ω)|)/dlog (ω) en fonction <strong>de</strong> δ/90 pour chaque température<br />
en considérant <strong>de</strong>ux fréquences voisines. La vérification comme le montre <strong>la</strong> figure 4.4 met en<br />
évi<strong>de</strong>nce l’approximation (4.4) proposée par Booij.<br />
Selon le principe d’équivalence temps-température, il existe un coefficient a(T1,T2) = f2/f1 = ω2/ω1<br />
<strong>de</strong> telle sorte que |E ∗ (T1,ω1)| = |E ∗ (T2,ω2)|.<br />
On peut donc réécrire l’équation (4.6) comme suit :<br />
δ moy 2<br />
(ω2). T1,T2 π = log (|E∗ (T1,ω2)|) − log (|E∗ (T2,ω2)|)<br />
log (a(T1,T2))<br />
avec δ moy<br />
T1,T2 (ω2) est <strong>la</strong> moyenne <strong>de</strong>s <strong>de</strong>ux angles mesurés aux températures T1 et T2 pour une pulsation<br />
ω2.<br />
(4.7)<br />
78