- Page 2:
The Philosophy of Mathematical Prac
- Page 6:
The Philosophyof MathematicalPracti
- Page 10:
PrefaceWhen in the spring of 2005 I
- Page 14:
ContentsBiographiesviiiIntroduction
- Page 18:
iographiesixJohannes Hafner is Assi
- Page 22: iographiesxiat the University of Pi
- Page 26: IntroductionThe essays contained in
- Page 30: introduction 31 Two traditionsMany
- Page 34: introduction 5A characterization in
- Page 38: introduction 7concerns. On the cont
- Page 42: introduction 9consists in trying to
- Page 46: introduction 11terms of their conse
- Page 50: introduction 13and epistemological
- Page 54: introduction 15classic that finally
- Page 58: introduction 17influenced by set-th
- Page 62: introduction 19in metaphyics when d
- Page 66: introduction 21Maddy, Penelope (199
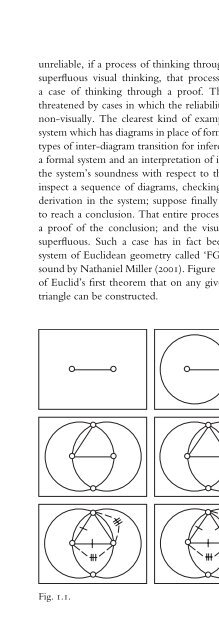
- Page 70: visualizing in mathematics 23Pasch
- Page 76: 26 marcus giaquintoMiller himself h
- Page 80: 28 marcus giaquintoTypically diagra
- Page 84: 30 marcus giaquintoclearly not enou
- Page 88: 32 marcus giaquintothe internal ang
- Page 92: 34 marcus giaquintoPythagoras’s t
- Page 96: 36 marcus giaquintofunction f (in t
- Page 100: 38 marcus giaquintorecall the puzzl
- Page 104: 40 marcus giaquintothinking is repl
- Page 108: 42 marcus giaquintoMancosu, Paolo(2
- Page 112: 44 marcus giaquintoof knowing struc
- Page 116: 46 marcus giaquintoorder-preserving
- Page 120: 48 marcus giaquintoA category speci
- Page 124:
50 marcus giaquintoWe name the bott
- Page 128:
52 marcus giaquintoinitial element
- Page 132:
54 marcus giaquintoAttention shifti
- Page 138:
cognition of structure 57infinite c
- Page 142:
cognition of structure 59with the s
- Page 146:
cognition of structure 61ordinal nu
- Page 150:
cognition of structure 63to merely
- Page 154:
3Diagram-Based GeometricPracticeKEN
- Page 158:
diagram-based geometric practice 67
- Page 162:
diagram-based geometric practice 69
- Page 166:
diagram-based geometric practice 71
- Page 170:
diagram-based geometric practice 73
- Page 174:
diagram-based geometric practice 75
- Page 178:
diagram-based geometric practice 77
- Page 182:
diagram-based geometric practice 79
- Page 186:
the euclidean diagram (1995) 81I su
- Page 190:
the euclidean diagram (1995) 834.1.
- Page 194:
the euclidean diagram (1995) 85of s
- Page 198:
the euclidean diagram (1995) 87both
- Page 202:
the euclidean diagram (1995) 89a di
- Page 206:
the euclidean diagram (1995) 91diag
- Page 210:
the euclidean diagram (1995) 93Exac
- Page 214:
the euclidean diagram (1995) 95APFi
- Page 218:
the euclidean diagram (1995) 97rela
- Page 222:
the euclidean diagram (1995) 99perh
- Page 226:
the euclidean diagram (1995) 101The
- Page 230:
the euclidean diagram (1995) 103and
- Page 234:
the euclidean diagram (1995) 105a p
- Page 238:
the euclidean diagram (1995) 107nev
- Page 242:
the euclidean diagram (1995) 109Thu
- Page 246:
the euclidean diagram (1995) 111A p
- Page 250:
the euclidean diagram (1995) 113Wha
- Page 254:
the euclidean diagram (1995) 115ADC
- Page 258:
the euclidean diagram (1995) 117We
- Page 262:
the euclidean diagram (1995) 119by
- Page 266:
the euclidean diagram (1995) 121of
- Page 270:
the euclidean diagram (1995) 123AFi
- Page 274:
the euclidean diagram (1995) 125by
- Page 278:
the euclidean diagram (1995) 127bra
- Page 282:
the euclidean diagram (1995) 129Eit
- Page 286:
the euclidean diagram (1995) 131gra
- Page 290:
the euclidean diagram (1995) 133Mue
- Page 294:
mathematical explanation: why it ma
- Page 298:
mathematical explanation: why it ma
- Page 302:
mathematical explanation: why it ma
- Page 306:
mathematical explanation: why it ma
- Page 310:
mathematical explanation: why it ma
- Page 314:
mathematical explanation: why it ma
- Page 318:
mathematical explanation: why it ma
- Page 322:
mathematical explanation: why it ma
- Page 326:
6Beyond UnificationJOHANNES HAFNER
- Page 330:
eyond unification 153initially appe
- Page 334:
eyond unification 155This example w
- Page 338:
eyond unification 157equations and
- Page 342:
eyond unification 159elementary pro
- Page 346:
eyond unification 161||x|| = √ x
- Page 350:
eyond unification 163cover also the
- Page 354:
eyond unification 165the necessary
- Page 358:
eyond unification 167consideration.
- Page 362:
eyond unification 169Now, can there
- Page 366:
eyond unification 171unification in
- Page 370:
eyond unification 173E I (K) comes
- Page 374:
eyond unification 175(3) F(ϕ) = 0
- Page 378:
eyond unification 177AppendixAxioms
- Page 382:
7Purity as an Ideal of ProofMICHAEL
- Page 386:
purity as an ideal of proof 181Ther
- Page 390:
purity as an ideal of proof 183Anal
- Page 394:
purity as an ideal of proof 185Late
- Page 398:
purity as an ideal of proof 187even
- Page 402:
purity as an ideal of proof 189conf
- Page 406:
purity as an ideal of proof 191adva
- Page 410:
purity as an ideal of proof 193is p
- Page 414:
purity as an ideal of proof 195Ewal
- Page 418:
purity as an ideal of proof 197Viè
- Page 422:
purity of method in hilbert’s gru
- Page 426:
purity of method in hilbert’s gru
- Page 430:
purity of method in hilbert’s gru
- Page 434:
purity of method in hilbert’s gru
- Page 438:
Two pages later, Hilbert remarks:pu
- Page 442:
purity of method in hilbert’s gru
- Page 446:
purity of method in hilbert’s gru
- Page 450:
purity of method in hilbert’s gru
- Page 454:
purity of method in hilbert’s gru
- Page 458:
purity of method in hilbert’s gru
- Page 462:
purity of method in hilbert’s gru
- Page 466:
purity of method in hilbert’s gru
- Page 470:
purity of method in hilbert’s gru
- Page 474:
purity of method in hilbert’s gru
- Page 478:
purity of method in hilbert’s gru
- Page 482:
purity of method in hilbert’s gru
- Page 486:
purity of method in hilbert’s gru
- Page 490:
purity of method in hilbert’s gru
- Page 494:
purity of method in hilbert’s gru
- Page 498:
purity of method in hilbert’s gru
- Page 502:
purity of method in hilbert’s gru
- Page 506:
purity of method in hilbert’s gru
- Page 510:
purity of method in hilbert’s gru
- Page 514:
purity of method in hilbert’s gru
- Page 518:
purity of method in hilbert’s gru
- Page 522:
purity of method in hilbert’s gru
- Page 526:
purity of method in hilbert’s gru
- Page 530:
purity of method in hilbert’s gru
- Page 534:
purity of method in hilbert’s gru
- Page 538:
mathematical concepts and definitio
- Page 542:
mathematical concepts and definitio
- Page 546:
mathematical concepts and definitio
- Page 550:
mathematical concepts and definitio
- Page 554:
mathematical concepts and definitio
- Page 558:
mathematical concepts and definitio
- Page 562:
mathematical concepts and definitio
- Page 566:
mathematical concepts and definitio
- Page 570:
mathematical concepts and definitio
- Page 574:
mathematical concepts and definitio
- Page 578:
mathematical concepts: fruitfulness
- Page 582:
mathematical concepts: fruitfulness
- Page 586:
mathematical concepts: fruitfulness
- Page 590:
mathematical concepts: fruitfulness
- Page 594:
mathematical concepts: fruitfulness
- Page 598:
mathematical concepts: fruitfulness
- Page 602:
mathematical concepts: fruitfulness
- Page 606:
mathematical concepts: fruitfulness
- Page 610:
mathematical concepts: fruitfulness
- Page 614:
mathematical concepts: fruitfulness
- Page 618:
mathematical concepts: fruitfulness
- Page 622:
mathematical concepts: fruitfulness
- Page 626:
mathematical concepts: fruitfulness
- Page 630:
computers in mathematical inquiry 3
- Page 634:
computers in mathematical inquiry 3
- Page 638:
computers in mathematical inquiry 3
- Page 642:
computers in mathematical inquiry 3
- Page 646:
computers in mathematical inquiry 3
- Page 650:
computers in mathematical inquiry 3
- Page 654:
computers in mathematical inquiry 3
- Page 658:
12Understanding ProofsJEREMY AVIGAD
- Page 662:
understanding proofs 319theorem is
- Page 666:
understanding proofs 321theorems, p
- Page 670:
understanding proofs 323of abilitie
- Page 674:
understanding proofs 325explain the
- Page 678:
understanding proofs 327possible to
- Page 682:
understanding proofs 329Ryle intend
- Page 686:
understanding proofs 331to explain,
- Page 690:
understanding proofs 333an ordinary
- Page 694:
understanding proofs 335that to exp
- Page 698:
understanding proofs 337value of k,
- Page 702:
understanding proofs 339integers in
- Page 706:
understanding proofs 341the use of
- Page 710:
understanding proofs 343know that b
- Page 714:
understanding proofs 345procedures
- Page 718:
understanding proofs 347on the firs
- Page 722:
understanding proofs 34912.9 Unders
- Page 726:
understanding proofs 351Mathematics
- Page 730:
understanding proofs 353Tiwari, A.(
- Page 734:
what structuralism achieves 355Phil
- Page 738:
what structuralism achieves 357that
- Page 742:
what structuralism achieves 359numb
- Page 746:
what structuralism achieves 361This
- Page 750:
what structuralism achieves 363Even
- Page 754:
what structuralism achieves 365get
- Page 758:
what structuralism achieves 367But
- Page 762:
what structuralism achieves 369Reid
- Page 766:
‘there is no ontology here’ 371
- Page 770:
‘there is no ontology here’ 373
- Page 774:
‘there is no ontology here’ 375
- Page 778:
‘there is no ontology here’ 377
- Page 782:
‘there is no ontology here’ 379
- Page 786:
‘there is no ontology here’ 381
- Page 790:
‘there is no ontology here’ 383
- Page 794:
‘there is no ontology here’ 385
- Page 798:
‘there is no ontology here’ 387
- Page 802:
‘there is no ontology here’ 389
- Page 806:
‘there is no ontology here’ 391
- Page 810:
‘there is no ontology here’ 393
- Page 814:
‘there is no ontology here’ 395
- Page 818:
‘there is no ontology here’ 397
- Page 822:
‘there is no ontology here’ 399
- Page 826:
‘there is no ontology here’ 401
- Page 830:
‘there is no ontology here’ 403
- Page 834:
‘there is no ontology here’ 405
- Page 838:
15The Boundary BetweenMathematics a
- Page 842:
the boundary between mathematics an
- Page 846:
the boundary between mathematics an
- Page 850:
the boundary between mathematics an
- Page 854:
the boundary between mathematics an
- Page 858:
16Mathematics and Physics:Strategie
- Page 862:
mathematics and physics: strategies
- Page 866:
mathematics and physics: strategies
- Page 870:
mathematics and physics: strategies
- Page 874:
mathematics and physics: strategies
- Page 878:
mathematics and physics: strategies
- Page 882:
mathematics and physics: strategies
- Page 886:
mathematics and physics: strategies
- Page 890:
mathematics and physics: strategies
- Page 894:
mathematics and physics: strategies
- Page 898:
mathematics and physics: strategies
- Page 902:
mathematics and physics: strategies
- Page 906:
Index of NamesAigner, M. 337, 351bA
- Page 910:
index of names 443Frege, G. ix-x, 7
- Page 914:
index of names 445McCune, W. 304, 3
- Page 918:
index of names 447Weiner, M. 71Weis