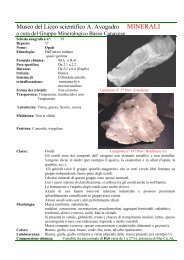
Geometria - Autistici

Spazio vettoriale 131
Da tener ben presente che queste somme sono dette formali perché sono da considerarsi appunto dei puri simboli. In
pratica gli elementi di B servono solo come "segnaposto" per i coefficienti. Oltre a questa definizione più intuitiva ne
esiste una del tutto equivalente in termine di funzioni da B su K con supporto finito (supp f := { b ∈ B | f(b) ≠ 0 }),
cioè V ≅ { f: B → K | supp f è finito } dove per il secondo insieme le operazioni di somma e prodotto sono quelle
naturali e la corrispondenza è
Arricchimenti della struttura di spazio vettoriale
La nozione di spazio vettoriale è servita innanzi tutto a puntualizzare proprietà algebriche riguardanti ambienti ed
entità geometriche; inoltre essa costituisce la base algebrica per lo studio di questioni di analisi funzionale, che
possiamo associare ad una geometrizzazione dello studio di funzioni collegate ad equazioni lineari. La sola struttura
di spazio vettoriale risulta comunque povera quando si vogliono affrontare in modo più efficace problemi geometrici
e dell'analisi funzionale. Infatti va osservato che con la sola struttura di spazio vettoriale non si possono affrontare
questioni riguardanti lunghezze di segmenti, distanze ed angoli (anche se la visione intuitiva degli spazi vettoriali a 2
o 3 dimensioni sembra implicare necessariamente queste nozioni di geometria elementare). Per sviluppare le
"potenzialità" della struttura spazio vettoriale risulta necessario arricchirla in molteplici direzioni, sia con ulteriori
strumenti algebrici (ad es. proponendo prodotti di vettori), sia con nozioni topologiche, sia con nozioni differenziali.
In effetti si può prospettare una sistematica attività di arricchimento degli spazi vettoriali con costruzioni che si
aggiungono a quella di combinazione lineare al fine di ottenere strutture di elevata efficacia nei confronti di tanti
problemi matematici, computazionali e applicativi. Per essere utili, queste costruzioni devono essere in qualche
modo compatibili con la struttura dello spazio vettoriale, e le condizioni di compatibilità variano caso per caso.
Spazio normato
Uno spazio vettoriale in cui è definita una norma, cioè una lunghezza dei suoi vettori, è chiamato spazio normato.
L'importanza degli spazi vettoriali normati dipende dal fatto che a partire dalla norma dei singoli vettori si definisce
la → distanza fra due vettori come norma della loro differenza e questa nozione consente di definire costruzioni
metriche e quindi costruzioni topologiche.
Spazio di Banach
Uno spazio normato completo rispetto alla metrica indotta è detto spazio di Banach.
Spazio di Hilbert
Uno spazio vettoriale complesso (risp. reale) in cui è definito un → prodotto scalare hermitiano (risp. bilineare)
definito positivo, e quindi anche i concetti di angolo e perpendicolarità di vettori, è chiamato spazio prehilbertiano.
Uno spazio dotato di prodotto scalare è anche normato, mentre in generale non vale il viceversa.
Uno spazio dotato di prodotto scalare che sia completo rispetto alla metrica indotta è detto spazio di Hilbert.
Spazio vettoriale topologico
Uno spazio vettoriale munito anche di una topologia è chiamato spazio vettoriale topologico.