Perspektiv på välfärden 2004 (pdf) - Statistiska centralbyrån

departs from the indicators that make up the deprivation
index, because it is not only dependent on
the respondents' interpretation of the situation, but
also on the fact that the situation has been evaluated
and that need for assistance has been confirmed.
Interpreting today from the rear view
The availability of longitudinal data represents a
great step forward for youth research, enabling
analysis of the long-term impact of conditions
during youth. However, longitudinal data have
one serious drawback, especially if they cover a
relatively long time span; they tempt us to draw
conclusions about today’s society based on conditions
that prevailed during an earlier period. To
mitigate this problem of relevancy, one strategy,
which is used here, is to base the analysis on aspects
that repeatedly, and over a long period of
time, have been shown to be important for the
structure of economic rewards and living conditions.
Another strategy is to place the analysis in a
historical context, comparing the conditions in
‘our’ cohort with the situation among today’s
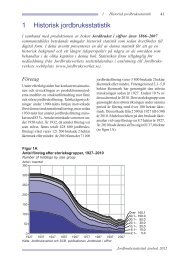
youth. 0Because ULF is an ongoing survey program,
a number of variables can be utilized in
time series. Figure 2 displays the difference in
unemployment, employment, lack of cash margin
and social assistance between 19- to 25-year-olds
and 35- to 41-year-olds between 1975 and 2001
(for social assistance 1983-2000). The young
group match our panel sample at t 0 , while the
older group is the same age as our panel sample at
t 2. As expected, the younger group is worse off
compared to the middle aged, but they follow the
same development and the ratio between the
groups is stable or in fact somewhat declining
over time. Deviating from this pattern is the employment
rate, such that the relative difference
between the age groups increases. However, this
increase is not related primarily to unemployment,
but to prolonged education among the young. It is
clear from Figure 2 that the recession in the 1990s
affected the situation for the young, but there is
nothing to indicate that the situation in the beginning
of the new millennium is dramatically worse
than it was 20 years ago.
Surveys are always affected by non-responses,
which is problematic when one suspects covariation
between non-responses and the key issue to
be investigated. It is, for example, reasonable to
expect that non-responses will be relatively common
among the poorest and most marginalized
section of the population. Hence, we can assume,
in the context of this study, that we underestimate
surveys reveals that the question underreports the ex-
tent of social assistance.
Youth
the extent to which young people suffer from
economic hardship. The problem is exaggerated
when longitudinal data are utilized, as we can also
assume a similar bias as regards panel attrition.
Because ULF uses a mix between a panel sample
and a cross-sectional sample, we can actually
analyse the degree to which our panel is affected
by attrition. Table 1 displays mean values not
only for the panel sample, but also for an age- and
year-matched cross-sectional sample. Here we can
see that the panel sample is somewhat wealthier
and less deprived compare to a cross-sectional
sample. A comparison between the panel and
cross-sectional data is also made in table1, revealing
the same pattern. Higher education is significantly
more common in the panel, while nest
leaving, parenthood and social assistance are
more frequent in the cross-sectional sample.
Hence, it can be concluded that the panel sample
will display a more favourable picture of the
youth situation compared with the cross-sectional
sample, which, in turn, is probably underestimating
the incidence of problems from the outset.
Method
To analyse our data, a so-called growth model has
been estimated (cf. Halleröd and Gustafsson
2003; McArdle 1988; Meredith and Tisak 1990;
Muthén and Khoo 1998; Rogosa, Brandt and Zimowski
1982). The basic idea of growth modelling
is to describe trajectories over time in terms
of parsimonious models. Using a structural equation
(SEM) framework, a latent variable is identified
through its relations to multiple observed
variables. The approach has several advantages.
The latent variable is not influenced by random
errors of measurement, separating actual change
from measurement errors. It allows formulation of
structural models, in which a particular assumed
pattern of influences among variables is tested
against empirical data (Hoyle 1995).
In the latent variable approach, the estimation
problem is to determine the parameters of the
distribution, i.e., mean and variance for a normal
distribution. In a linear growth model, one latent
variable represents individual differences in intercept
parameters, while another latent variable
represents individual differences in slope parameters.
The estimation of a growth model from three
observations of income includes two latent variables:
Intercept and Slope. The Intercept variable
represents individual differences in income at t 0
and has a fixed relation of unity to all three manifest
variables (i.e., observed income at t 0, t 1, and t 2) .
The Slope variabl0e represents individual differences
in change in income over time. In a linear
model, the Slope variable has a fixed relation of 0
with the t 0 measure, of 1 with the t 1 measure, and
of 2 with the t 2 measure, expressing the assump-
73