Noter til E6 - dirac

More documents

Recommendations

Info

$Guide to Imfufa LaTeX - dirac$

54 Nogle eksempler dagsordenen er at undersøge om modellen kan forsimples. Eksempelvis kan man undersøge om de to kurver er parallelle, og hvis det kan accepteres, kan man derefter undersøge om kurverne er sammenfaldende. Vi formulerer derfor to statistiske hypoteser: 1. Hypotesen om parallelle kurver: H 1 : β M = β F , eller mere udførligt: Der findes konstanter α M , α F og β således at logit(p dM ) = α M + β ln d logit(p dF ) = α F + β ln d. 2. Hypotesen om sammenfaldende kurver: H 2 : α M = α F og β M = β F , eller mere udførligt: Der findes konstanter α og β således at logit(p dM ) = α + β ln d logit(p dF ) = α + β ln d. Vi undersøger først hypotesen H 1 om parallelle kurver. Maksimaliseringsestimaterne er ̂α M = 3.835 (med en middelfejl på 0.3443), ̂α F = 2.831 (middelfejl 0.3105) og ̂β = 2.813 (middelfejl 0.2386). Hypotesen testes med det sædvanlige kvotienttest hvor man sammenligner den maksimale likelihoodfunktion under antagelse af H 1 med den maksimale likelihoodfunktion i den senest accepterede model: −2 ln Q = −2 ln L(̂α M , ̂α F , ̂β, ̂β) L(̂α M , ̂α F , ̂β M , ̂β F ) = 2 ∑ ( ) ∑ y dk ln ŷdk + (n dk − y dk ) ln n dk − ŷ dk k d ŷ dk n dk − ŷ dk hvor ŷ dk = n dk exp(bα k + b β ln d) 1+exp(bα k + b β ln d) . Man får at −2 ln Q obs = 1.3067, der skal sammenlignes med χ 2 -fordelingen med 4 − 3 = 1 frihedsgrader (ændring i antal parametre). Testsandsynligheden (dvs. sandsynligheden for at få værdier større end 1.3067) er ca. 25%, dvs. værdien 1.3067 er ikke usædvanligt stor. Modellen med parallelle kurver giver således ikke en signifikant dårligere beskrivelse af observationerne end den hidtidige model gør. Efter således at have accepteret hypotesen H 1 kan vi gå videre med hypotesen H 2 om sammenfaldende kurver. (Hvis H 1 var blevet forkastet, ville man ikke gå videre til H 2 .) Når man tester H 2 i forhold til H 1 , får man −2 ln Q obs = 27.5017 der skal sammenlignes med χ 2 -fordelingen med et antal frihedsgrader på 3−2 = 1; sandsynligheden for at få værdier større end 27.5017 er lig nul med adskillige betydende cifre, hvilket viser at modellen med sammenfaldende kurver giver en væsentligt dårligere beskrivelse af observationerne end den forrige model gør. Vi må derfor forkaste hypotesen om sammenfaldende kurver.
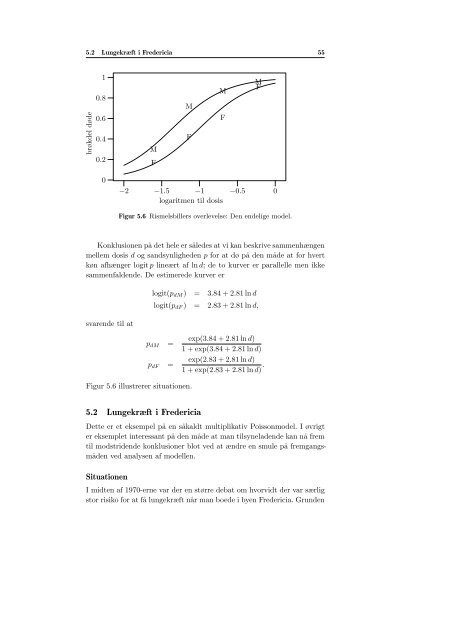
5.2 Lungekræft i Fredericia 55 brøkdel døde 1 0.8 0.6 0.4 0.2 M F M F M F M F 0 −2 −1.5 −1 −0.5 0 logaritmen til dosis Figur 5.6 Rismelsbillers overlevelse: Den endelige model. Konklusionen på det hele er således at vi kan beskrive sammenhængen mellem dosis d og sandsynligheden p for at dø på den måde at for hvert køn afhænger logit p lineært af ln d; de to kurver er parallelle men ikke sammenfaldende. De estimerede kurver er svarende til at logit(p dM ) = 3.84 + 2.81 ln d logit(p dF ) = 2.83 + 2.81 ln d, p dM = p dF = exp(3.84 + 2.81 ln d) 1 + exp(3.84 + 2.81 ln d) exp(2.83 + 2.81 ln d) 1 + exp(2.83 + 2.81 ln d) . Figur 5.6 illustrerer situationen. 5.2 Lungekræft i Fredericia Dette er et eksempel på en såkaldt multiplikativ Poissonmodel. I øvrigt er eksemplet interessant på den måde at man tilsyneladende kan nå frem til modstridende konklusioner blot ved at ændre en smule på fremgangsmåden ved analysen af modellen. Situationen I midten af 1970-erne var der en større debat om hvorvidt der var særlig stor risiko for at få lungekræft når man boede i byen Fredericia. Grunden
Page 1 and 2:
Noter til E6 Del 2: Statistik Jørg
Page 3 and 4:
Indhold 1 Indledning 3 2 Den statis
Page 5 and 6: 1 Indledning Hvor sandsynlighedsreg
Page 7 and 8: 2 Den statistiske model Vi vil før
Page 9 and 10: 2.1 Eksempler 7 Den simple binomial
Page 11 and 12: 2.1 Eksempler 9 Tabel 2.2 Rismelsbi
Page 13 and 14: 2.1 Eksempler 11 Tabel 2.3 Genotype
Page 15 and 16: 2.1 Eksempler 13 tionen er n∏ f(y
Page 17 and 18: 2.1 Eksempler 15 observationer grup
Page 19 and 20: 2.2 Opgaver 17 Tabel 2.6 Forbes’
Page 21 and 22: 3 Estimation En statistisk model er
Page 23 and 24: 3.2 Eksempler 21 asymptotisk varian
Page 25 and 26: 3.2 Eksempler 23 Eksempel 3.2 (Rism
Page 27 and 28: 3.2 Eksempler 25 I Poissonfordeling
Page 29 and 30: 3.2 Eksempler 27 med 63 frihedsgrad
Page 31 and 32: 3.2 Eksempler 29 idet de øvrige to
Page 33: 3.3 Opgaver 31 3.3 Opgaver Opgave 3
Page 36 and 37: 34 Hypoteseprøvning eller mere udf
Page 38 and 39: 36 Hypoteseprøvning Eksempel 4.1 (
Page 40 and 41: 38 Hypoteseprøvning Tabel 4.1 Rism
Page 42 and 43: 40 Hypoteseprøvning hvor by 1 = 69
Page 44 and 45: 42 Hypoteseprøvning Vi har tidlige
Page 46 and 47: 44 Hypoteseprøvning forhånd kan s
Page 49 and 50: 5 Nogle eksempler 5.1 Rismelsbiller
Page 51 and 52: 5.1 Rismelsbiller 49 brøkdel døde
Page 53 and 54: 5.1 Rismelsbiller 51 3 M logit(brø
Page 55: 5.1 Rismelsbiller 53 brøkdel døde
Page 59 and 60: 5.2 Lungekræft i Fredericia 57 Tab
Page 61 and 62: 5.2 Lungekræft i Fredericia 59 = k
Page 67 and 68: 5.2 Lungekræft i Fredericia 65 Her
Page 69 and 70: 5.3 Ulykker på en granatfabrik 67
Page 75 and 76: 6 Den flerdimensionale normalfordel
Page 77 and 78: 6.2 Definition og egenskaber 75 6.2
Page 79 and 80: 6.2 Definition og egenskaber 77 Sæ
Page 81: 6.2 Definition og egenskaber 79 og
Page 84 and 85: 82 Lineære normale modeller ◦ De
Page 86 and 87: 84 Lineære normale modeller Hypote
Page 88 and 89: 86 Lineære normale modeller Tabel
Page 90 and 91: 88 Lineære normale modeller skal h
Page 92 and 93: 90 Lineære normale modeller samme
Page 94 and 95: 92 Lineære normale modeller gjaldt
Page 96 and 97: 94 Lineære normale modeller og alt
Page 98 and 99: 96 Lineære normale modeller Tabel
Page 100 and 101: 98 Lineære normale modeller Hvis m
Page 102 and 103: 100 Lineære normale modeller varia
Page 104 and 105: 102 Lineære normale modeller og no
Page 106 and 107:
104 Lineære normale modeller Konce
Page 108 and 109:
106 Lineære normale modeller Opgav
Page 110 and 111:
108
Page 112 and 113:
110 En udledning af normalfordeling
Page 114 and 115:
112
Page 116 and 117:
114 Nogle resultater fra lineær al
Page 118 and 119:
116
Page 120 and 121:
118 Tabeller Fraktiler i χ 2 -ford
Page 122 and 123:
120 Tabeller 90% fraktiler i F -for
Page 124 and 125:
122 Tabeller 97.5% fraktiler i F -f
Page 126 and 127:
124 Tabeller Fraktiler i t-fordelin
Page 128 and 129:
126
Page 130 and 131:
128 Stikord - middelværdi 73 - var
show all

Noter til E6 - dirac

You also want an ePaper? Increase the reach of your titles

Delete template?

Save as template?