Helle atomare Solitonen - KOPS - Universität Konstanz

78 KAPITEL 3. THEORIE
a
1
|f | 2 [a.u.]
b
|f | 2 [a.u.] scharzes Soliton
graues Soliton
T=0 T>0
0
/2
Phase@T=0
Zeit[a.u.]
/2
x[a.u.]
x[a.u.]
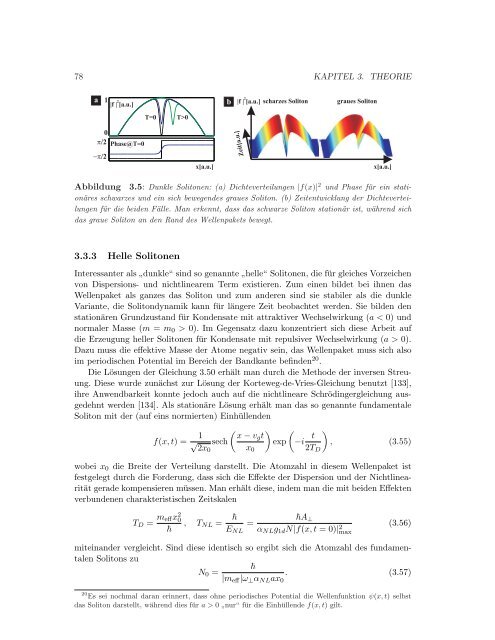
Abbildung 3.5: Dunkle Solitonen: (a) Dichteverteilungen |f(x)| 2 und Phase für ein stationäres
schwarzes und ein sich bewegendes graues Soliton. (b) Zeitentwicklung der Dichteverteilungen
für die beiden Fälle. Man erkennt, dass das schwarze Soliton stationär ist, während sich
das graue Soliton an den Rand des Wellenpakets bewegt.
3.3.3 Helle Solitonen
Interessanter als ”
dunkle“ sind so genannte ”
helle“ Solitonen, die für gleiches Vorzeichen
von Dispersions- und nichtlinearem Term existieren. Zum einen bildet bei ihnen das
Wellenpaket als ganzes das Soliton und zum anderen sind sie stabiler als die dunkle
Variante, die Solitondynamik kann für längere Zeit beobachtet werden. Sie bilden den
stationären Grundzustand für Kondensate mit attraktiver Wechselwirkung (a < 0) und
normaler Masse (m = m 0 > 0). Im Gegensatz dazu konzentriert sich diese Arbeit auf
die Erzeugung heller Solitonen für Kondensate mit repulsiver Wechselwirkung (a > 0).
Dazu muss die effektive Masse der Atome negativ sein, das Wellenpaket muss sich also
im periodischen Potential im Bereich der Bandkante befinden 20 .
Die Lösungen der Gleichung 3.50 erhält man durch die Methode der inversen Streuung.
Diese wurde zunächst zur Lösung der Korteweg-de-Vries-Gleichung benutzt [133],
ihre Anwendbarkeit konnte jedoch auch auf die nichtlineare Schrödingergleichung ausgedehnt
werden [134]. Als stationäre Lösung erhält man das so genannte fundamentale
Soliton mit der (auf eins normierten) Einhüllenden
f(x, t) = √ 1 ( ) ( )
x − vg t
t
sech
exp −i , (3.55)
2x0 x 0 2T D
wobei x 0 die Breite der Verteilung darstellt. Die Atomzahl in diesem Wellenpaket ist
festgelegt durch die Forderung, dass sich die Effekte der Dispersion und der Nichtlinearität
gerade kompensieren müssen. Man erhält diese, indem man die mit beiden Effekten
verbundenen charakteristischen Zeitskalen
T D = m effx 2 0
, T NL =
E NL
=
A ⊥
α NL g 1d N|f(x, t = 0)| 2 max
(3.56)
miteinander vergleicht. Sind diese identisch so ergibt sich die Atomzahl des fundamentalen
Solitons zu
N 0 =
. (3.57)
|m eff |ω ⊥ α NL ax 0
20 Es sei nochmal daran erinnert, dass ohne periodisches Potential die Wellenfunktion ψ(x, t) selbst
das Soliton darstellt, während dies für a > 0 ”
nur“ für die Einhüllende f(x, t) gilt.