Skripten - an der Fakultät für Mathematik! - Universität Wien

124 6. ZAHLENMENGEN
Wir haben schon nachgerechnet, dass i 2 = −1 gilt, und es folgt aus der Struktur von
=Ê×Êund der komponentenweisen Definition der Addition, dass sich jedes Element
(a 1 , a 2 ) voneindeutig schreiben lässt als (a 1 , a 2 ) = (a 1 , 0) + a 2 (0, 1) oder mit Hilfe der
Abkürzungen aus Definition 6.5.3 als (a 1 , a 2 ) = a 1 + ia 2 .
Damit gewinnen wir Eulers Schreibweise für die komplexen Zahlen zurück. Mythisches
oder Philosophisches haben wir dazu nicht benötigt. Wir fassen unsere neue Notation zusammen
und definieren.
Definition 6.5.4 (Real- und Imaginärteil). Sei z = (x, y) ∈. Dann schreiben wir z
auch als
z = x + iy
und bezeichnen x als den Realteil und y als den Imaginärteil von z und schreiben x = Rez =
Rz bzw. y = Im z = Iz.
Die komplexen Zahlen lassen sich als Elemente vonÊ×Ê=Ê2 klarerweise auch als
Punkte in der Ebene deuten. Das führt auf die Definition von Wessel, Argand und Gauss.
Auch die Polarkoordinatenrepräsentation durch Länge und Winkel ist auf diese geometrische
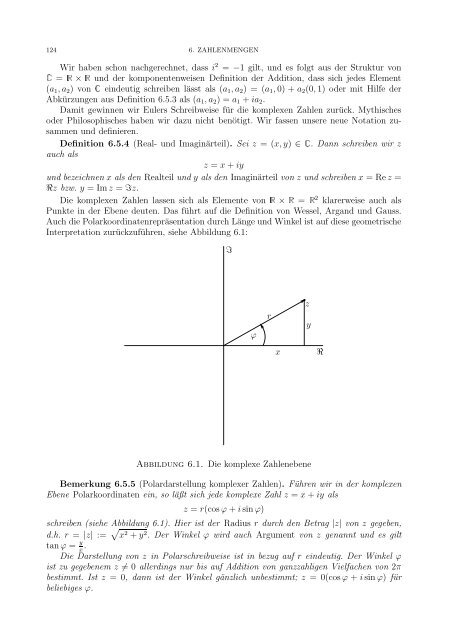
Interpretation zurückzuführen, siehe Abbildung 6.1:
I
ϕ
r
x
z
y
R
Abbildung 6.1. Die komplexe Zahlenebene
Bemerkung 6.5.5 (Polardarstellung komplexer Zahlen). Führen wir in der komplexen
Ebene Polarkoordinaten ein, so läßt sich jede komplexe Zahl z = x + iy als
z = r(cosϕ + i sin ϕ)
schreiben (siehe Abbildung 6.1). Hier ist der Radius r durch den Betrag |z| von z gegeben,
d.h. r = |z| := √ x 2 + y 2 . Der Winkel ϕ wird auch Argument von z genannt und es gilt
tanϕ = y x .
Die Darstellung von z in Polarschreibweise ist in bezug auf r eindeutig. Der Winkel ϕ
ist zu gegebenem z ≠ 0 allerdings nur bis auf Addition von ganzzahligen Vielfachen von 2π
bestimmt. Ist z = 0, dann ist der Winkel gänzlich unbestimmt; z = 0(cosϕ + i sin ϕ) für
beliebiges ϕ.