Skripten - an der Fakultät für Mathematik! - Universität Wien

58 4. MENGENLEHRE
gleich sind. Die durch f gegebene ”
Zuordnung“ kann deshalb als spezielle Teilmenge des
Produkts A × B beschrieben werden. Genau das macht sich die folgende Definition zunutze.
Definition 4.3.3 (Mengentheoretische Definition des Funktionsbegriffs). Eine Funktion
ist ein Tripel f = (A, B, G) bestehend aus einer Menge A, genannt Definitionsbereich,
einer Menge B, genannt Zielbereich und einer Teilmenge G des Produkts A × B mit den
Eigenschaften
(1) ∀a ∈ A ∃b ∈ B : (a, b) ∈ G
(D.h. jedes a ∈ A tritt als erste Komponente eines Paares in G auf.)
(2) ∀a ∈ A ∀b 1 , b 2 ∈ B : (a, b 1 ) ∈ G ∧ (a, b 2 ) ∈ G ⇒ b 1 = b 2
(D.h. stimmen die ersten Komponenten eines Paares in G überein, dann auch die
zweiten.)
Die Menge G heißt Graph der Funktion f und wird oft auch mit G(f) bezeichnet. Gilt
(a, b) ∈ G, so schreiben wir f(a) = b und wir können den Graphen schreiben als
G(f) = {(a, f(a))|a ∈ A}.
Die Paarungen (a, f(a)) sind gewissermaßen das abstrakte Analogon zur Zusammenstellung
der a-Werte und der zugehörigen Funktionswerte f(a) in einer Wertetabelle oder der
graphischen Darstellung der Funktion als “Kurve“ in einem kartesischen Koordinatensystem
(falls A und B Teilmengen vonÊsind); zwei Konzepte, die Ihnen sicherlich aus der Schule
ein Begriff sind.
Vielleicht haben Sie bemerkt, dass wir noch immer nicht gesagt haben, was eine ”
Zuordnung“
denn eigentlich ist. Die moderne Mathematik zieht sich in dieser und ähnlichen
Situationen aus der Affäre, indem Sie Ihnen die Objekte ”
aufzählt“, die einander ”
zugeordnet“
sind; in unserem Fall die geordneten Paare (a, f(a)).
Nach dieser ”
philosophischen“ Bemerkung kommen wir zu einem einfachen, konkreten
Beispiel.
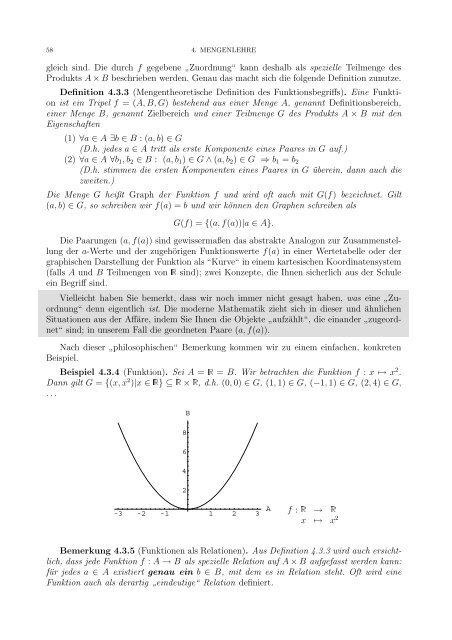
Beispiel 4.3.4 (Funktion). Sei A =Ê=B. Wir betrachten die Funktion f : x ↦→ x 2 .
Dann gilt G = {(x, x 2 )|x ∈Ê} ⊆Ê×Ê, d.h. (0, 0) ∈ G, (1, 1) ∈ G, (−1, 1) ∈ G, (2, 4) ∈ G,
. . .
8
B
6
4
2
-3 -2 -1 1 2 3 A
:Ê→Ê f
x ↦→ x 2
Bemerkung 4.3.5 (Funktionen als Relationen). Aus Definition 4.3.3 wird auch ersichtlich,
dass jede Funktion f : A → B als spezielle Relation auf A × B aufgefasst werden kann:
für jedes a ∈ A existiert genau ein b ∈ B, mit dem es in Relation steht. Oft wird eine
Funktion auch als derartig ”
eindeutige“ Relation definiert.