Prognosemetoder – en oversikt - Telenor

med en servomekanisme, lar den seg likevel
forstå: I en servomekanisme korrigeres
det for avviket (feilen) i forhold til
den fastsatte kurs og ikke for hva kursen
faktisk er.
Den matematiske formulering (3),
beskriver y ved q forutgående a-verdier
(og at ). Vi sier da at y kan beskrives ved
en MA-prosess av q-te orden og skriver
dette kort som MA(q).
I de fleste praktiske situasjoner vil antall
verdier av forutgående restledd, dvs q,
sjelden overstige 2. I så fall sier vi at vi
har en MA-prosess av andre orden og
skriver MA(2). (3) blir da slik:
yt = a1 - θ1at-1 - θ2at-2 (4)
Tilsvarende vil en MA-prosess av første
orden kun ha en forutgående a- verdi (+
at ) og bli betegnet med AR(1).
I tidsserier med sesongvariasjoner kan
den glidende gjennomsnittsbeskrivelse
lett utvides til å beskrive den siste tidsserieverdien
som en funksjon av restleddsverdier
en, to, tre, ..., osv sesonger
før. Da benytter vi store greske bokstaver
med fotskrift som refererer seg til antall
sesonger for parametrene, f eks Θ1 for
sesong en, og fotskrift t-s, t-2s, t-3s, ...,
for støyleddene hhv 1, 2, 3, ..., sesonger
bakover. s er her sesonglengden.
4 Autoregressiv-glidende
gjennomsnittsprosess
I praksis finnes det også mange tilfeller
av tidsrekker med både AR- og MA-prosesser
(såkalte ARMA-prosesser) og
disse refereres ofte til som miksede eller
blandede prosesser. Matematisk
uttrykkes dette ved en kombinasjon av
(1) og (3):
y t - φ 1 y t-1 - ... - φ p y t-p
= a t - θ 1 a t-1 - ... - θ q a t-q
hvor φ-ene og θ-ene er som beskrevet i
kapittel 3 og 4. Ved å flytte alle y-ene i
forutgående perioder over på høyre side
av likhetstegnet, får vi
y t = φ 1 y t-1 + ... + φ p y t-p
+ a t - θ 1 a t-1 - ... - θ q a t-q
(5)
(5)'
Vi ser altså at y er en funksjon av p tidligere
observasjoner og støyleddene i q
tidligere perioder. Vi sier da at y kan
beskrives ved en ARMA-prosess av
orden p og q. Som kort form skrives dette
ARMA(p,q).
I praksis vil vi også her oppleve at antall
parametre sjelden overstiger 2 av hhv AR
og MA. I så fall har vi sjelden mer enn en
ARMA(2,2)-prosess. (5) ser da slik ut:
y t - θ 1 y t-1 - θ 2 y t-2 = a t - θ 1 a t-1 - θ 2 a t-2
(6)
Tilsvarende kan vi ha ARMA-prosesser
med ARMA(1,2), ARMA(2,1) og
ARMA(1,1). Ved lavere orden reduseres
ARMA-prosessen naturlig nok til en ren
AR- eller MA-prosess.
5 Stasjonæritet
For å beskrive avhengigheten i en tidsserie
ved hjelp av AR-, MA- eller
ARMA-prosesser, må tidsserien først
være stasjonær. Et annet uttrykk for dette
kan være “statistisk likevekt”. Hvis tidsserien
i utgangspunktet ikke er stasjonær,
må den først transformeres eller
omformes slik at den blir det.
Uten å gå inn på den statistiske definisjon,
kan vi si at en stasjonær tidsrekke
har disse egenskapene:
- Konstant varians
- Ingen trend: tidsserien skal svinge
rundt et konstant nivå
- Ingen regulær sesongkomponent.
Vi skal nå se på hvordan vi behandler en
tidsrekke slik at den blir stasjonær. Vari-
(Mottatte bestillinger x 100)
51
41
31
21
ans-stabilitet oppnås ved en passende
transformasjon av data, mens fjerning av
trend og regulær sesongkomponent
gjøres ved differensiering av tidsrekken.
(Metoden kan strengt tatt også benyttes
uten at sesongkomponenten er fjernet.)
5.1 Stabilisering av variansen
Ofte har tidsrekker varians som ikke er
stabil over hele måleperioden. Et
eksempel er akkumulerte data; vi får i
mange tilfeller økende varians med
økende nivå. I så fall må vi foreta en
transformasjon av data, slik at variansen
stabiliseres. Det mest vanlige er å ta
logaritmen til tidsserien. Dette “krymper”
variasjonen i observasjonene, men da på
en slik måte at store verdier blir krympet
mer enn små. Eksempel på hvilken effekt
en slik transformasjon har på et valgt
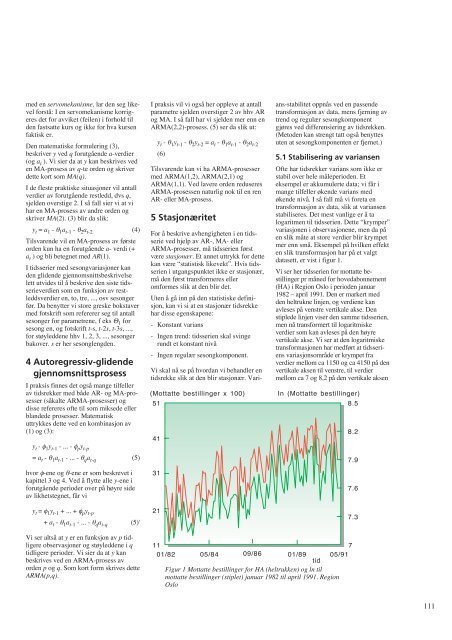
datasett, er vist i figur 1.
Vi ser her tidsserien for mottatte bestillinger
pr måned for hovedabonnement
(HA) i Region Oslo i perioden januar
1982 – april 1991. Den er markert med
den heltrukne linjen, og verdiene kan
avleses på venstre vertikale akse. Den
stiplede linjen viser den samme tidsserien,
men nå transformert til logaritmiske
verdier som kan avleses på den høyre
vertikale akse. Vi ser at den logaritmiske
transformasjonen har medført at tidsseriens
variasjonsområde er krympet fra
verdier mellom ca 1150 og ca 4150 på den
vertikale aksen til venstre, til verdier
mellom ca 7 og 8,2 på den vertikale aksen
In (Mottatte bestillinger)
8.5
11
7
01/82 05/84 09/86 01/89
tid
05/91
Figur 1 Mottatte bestillinger for HA (heltrukken) og ln til
mottatte bestillinger (stiplet) januar 1982 til april 1991. Region
Oslo
8.2
7.9
7.6
7.3
111