Prognosemetoder – en oversikt - Telenor

More documents

Recommendations

Info

114 AR-parametre og q MA-parametre beskrives kort slik: ARIMA(p,d,q). Hvis det i tillegg er behov for å modellere sesongsvingninger, er den generelle kortversjonen: ARIMA(p,d,q)X(P,D,Q). Her referer p, d og q til den sesonguavhengige delen av modellen, slik som i avsnittet ovenfor. P, D og Q i den andre parentesen beskriver den sesongmessige delen av modellen: P AR-parametere for beskrivelse av sesong, D sesongdifferensieringer og Q MA-parametere for beskrivelse av sesong. 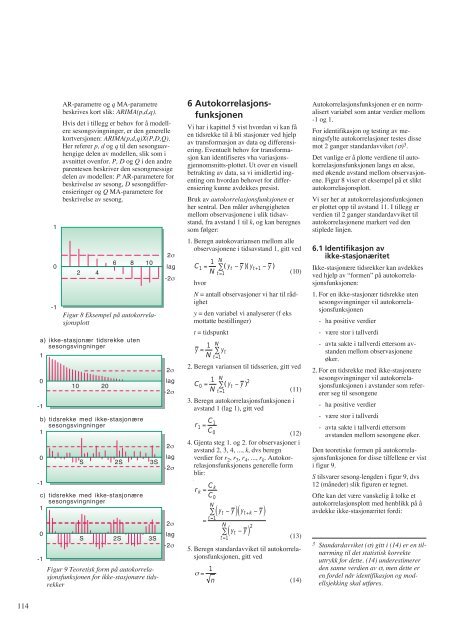a) ikke-stasjonær tidsrekke uten sesongsvingninger 1 0 -1 0 -1 0 1 0 -1 2 4 10 20 6 8 10 Figur 8 Eksempel på autokorrelasjonsplott b) tidsrekke med ikke-stasjonære sesongsvingninger 1 S 2S 3S c) tidsrekke med ikke-stasjonære sesongsvingninger 1 S 2S 3S -1 Figur 9 Teoretisk form på autokorrelasjonsfunksjonen for ikke-stasjonære tidsrekker 2σ lag -2σ 2σ lag -2σ 2σ lag -2σ 2σ lag -2σ 6 Autokorrelasjonsfunksjonen Vi har i kapittel 5 vist hvordan vi kan få en tidsrekke til å bli stasjonær ved hjelp av transformasjon av data og differensiering. Eventuelt behov for transformasjon kan identifiseres vha variasjonsgjennomsnitts-plottet. Ut over en visuell betrakting av data, sa vi imidlertid ingenting om hvordan behovet for differensiering kunne avdekkes presist. Bruk av autokorrelasjonsfunksjonen er her sentral. Den måler avhengigheten mellom observasjonene i ulik tidsavstand, fra avstand 1 til k, og kan beregnes som følger: 1. Beregn autokovariansen mellom alle observasjonene i tidsavstand 1, gitt ved C1 = (10) hvor N = antall observasjoner vi har til rådighet y = den variabel vi analyserer (f eks mottatte bestillinger) t = tidspunkt 1 N ( yt − y )( y N ∑ t+1 − y ) t=1 y = 1 N y N ∑ t t=1 2. Beregn variansen til tidsserien, gitt ved C0 = (11) 3. Beregn autokorrelasjonsfunksjonen i avstand 1 (lag 1), gitt ved 1 N ( y N ∑ t − y )2 t=1 r1 = (12) 4. Gjenta steg 1. og 2. for observasjoner i avstand 2, 3, 4, ..., k, dvs beregn verdier for r2 , r3 , r4 , ..., rk . Autokorrelasjonsfunksjonens generelle form blir: C1 C0 r k = (13) 5. Beregn standardavviket til autokorrelasjonsfunksjonen, gitt ved Ck C0 N ∑( yt − y ) ( yt+k − y ) t=1 = ( yt − y ) 2 N ∑ t=1 σ = 1 n (14) Autokorrelasjonsfunksjonen er en normalisert variabel som antar verdier mellom -1 og 1. For identifikasjon og testing av meningsfylte autokorrelasjoner testes disse mot 2 ganger standardavviket (σ) 3 . Det vanlige er å plotte verdiene til autokorrelasjonsfunksjonen langs en akse, med økende avstand mellom observasjonene. Figur 8 viser et eksempel på et slikt autokorrelasjonsplott. Vi ser her at autokorrelasjonsfunksjonen er plottet opp til avstand 11. I tillegg er verdien til 2 ganger standardavviket til autokorrelasjonene markert ved den stiplede linjen. 6.1 Identifikasjon av ikke-stasjonæritet Ikke-stasjonære tidsrekker kan avdekkes ved hjelp av “formen” på autokorrelasjonsfunksjonen: 1. For en ikke-stasjonær tidsrekke uten sesongsvingninger vil autokorrelasjonsfunksjonen - ha positive verdier - være stor i tallverdi - avta sakte i tallverdi ettersom avstanden mellom observasjonene øker. 2. For en tidsrekke med ikke-stasjonære sesongsvingninger vil autokorrelasjonsfunksjonen i avstander som refererer seg til sesongene - ha positive verdier - være stor i tallverdi - avta sakte i tallverdi ettersom avstanden mellom sesongene øker. Den teoretiske formen på autokorrelasjonsfunksjonen for disse tilfellene er vist i figur 9. S tilsvarer sesong-lengden i figur 9, dvs 12 (måneder) slik figuren er tegnet. Ofte kan det være vanskelig å tolke et autokorrelasjonsplott med henblikk på å avdekke ikke-stasjonæritet fordi: 3 Standardavviket (σ) gitt i (14) er en tilnærming til det statistisk korrekte uttrykk for dette. (14) underestimerer den sanne verdien av σ, men dette er en fordel når identifikasjon og modellsjekking skal utføres.
- Både ikke-stasjonæritet pga sesongsvingninger og utenom sesongsvingningene kan være til stede, noe som gir opphav til en blanding av de typene av autokorrelasjonsfunksjonene som er beskrevet i figur 9. I så fall vil autokorrelasjonsfunksjonen ha form som i figur 10a). - Signifikante autokorrelasjoner (dvs autokorrelasjoner større enn 2 ganger standardavviket) kan være til stede utenom sesong-lengden. Dette kompliserer tolkningen av ikke-stasjonære sesongsvingninger, se figur 10b). Etter at ikke-stasjonæritet er identifisert gjennom formen på autokorrelasjonsfunksjonen, bringes tidsrekken over på en stasjonær form ved å differensiere den en eller flere ganger, slik vi har vist i kapittel 5.2. I praksis bør en være oppmerksom på følgende: a. Autokorrelasjonsfunksjonen bør beregnes for så lang avstand mellom observasjonene at dens ikke-stasjonæritet blir avdekket. Dette kan gjøres ved å beregne den opp til avstand 15–20 for tidsrekker uten ikke-stasjonære sesongsvingninger og 3 ganger sesong (+1 observasjon) for tidsrekker med ikke-stasjonære sesongsvingninger. b. Det er i teorien ingen grenser for hvor mange ganger en tidsrekke bør differensieres for å bringe den over på stasjonær form. I praksis er det likevel uvanlig med mer enn to ikke-sesongavhengige differensieringer og en sesongavhengig differensiering. c. Mistolkning av autokorrelasjonsfunksjonen kan lede til over-differensiering. En tidsserie som går mot stasjonær tilstand vil redusere sin varians, mens over-differensiering øker variansen. 6.2 Eksempel I kapittel 5.1 så vi hvordan vi kunne identifisere hvorvidt mottatte bestillinger i Region Oslo hadde konstant varians. Vi så på variasjons-gjennomsnitts-plottet og fant at en ln-transformasjon av data stabiliserte variansen. I dette eksempelet er denne transformasjonen foretatt. For å identifisere eventuelt behov for differensiering starter vi med å plotte autokorrelasjonsfuksjonen for den ln-transformerte tidsrekken, se figur 11. Vi ser klart at formen på autokorrelasjonsfunksjonen likner på figur 9a), bortsett fra at den etter hvert kryper under 0. Dette er et klart tegn på at tidsrekken har en trend, slik dette ble beskrevet under kapittel 5.2, og at det er behov for differensiering. I tillegg ser vi at formen på autokorrelasjonsfunksjonen er noe bueformet, slik som i figur 10a). Dette er et tegn på at det også kan være behov for sesong-differensiering. I figur 12 er tidsserien differensiert en gang. Vi ser tydelig at indikasjonene på behov for differensiering pga trend er borte. Tilbake står signifikante (de er større enn 2 ganger standardavviket) autokorrelasjoner i avstand 12, dvs slik som i figur 9b). I tillegg ser vi enkelte andre store autokorrelasjoner. Noen av disse har klart form av figur 10b). Det er altså behov for å differensiere tidsserien en gang til, men nå mhp sesong. I figur 13 er tidsserien også differensiert en gang mhp sesong. Vi ser nå tydelig at formen på autokorrelasjonsfunksjonen ikke har noen av de “mønstre” som vi beskrev i figur 9 og 10. Det er m a o store muligheter for at tidsserien er stasjonær. Tilbake står noen få autokorrelasjoner som er større enn 2 ganger standardavviket. Disse kommer vi tilbake til under modelleringen nedenfor. Resten har karakter av å være tilfeldig. 6.3 Identifikasjon av AR- og MA-prosesser i en stasjonær tidsserie En stasjonær tidsserie vil som regel fremdeles være autokorrelert, ref de signifikante autokorrelasjonene i figur 13. Derfor har vi behov for å “fjerne” denne korrelasjonen ved å modellere den med AR- og MA-prosesser, slik at vi står igjen med støyledd som er uavhengige, dvs at det ikke er noe autokorrelasjon tilbake, ref forutsetningene om støyleddene i kapittel 2. Før vi analyserer de signifikante autokorrelasjonene i en stasjonær tidsrekke bør vi også huske at selv i en tilfeldig tidsrekke, dvs en tidsrekke uten noe autokorrelasjon, vil vi vanligvis finne at 1 av 20 (5 %) autokorrelasjoner er signifikante når grensen for signifikans er 2 ganger standardavviket4 . Det vi må spørre oss om er om autokorrelasjonene er meningsfylte: 1. Signifikante autokorrelasjoner for observasjoner med liten avstand er en indikasjon på ikke-sesongavhengig eller periode til periode-prosesser. 2. Signifikante autokorrelasjoner med avstand lik sesongperiodene eller 1, 2, a) tidsrekke med ikke-stasjonæritet pga av sesongsvingninger og utenom sesongsvingninger 1 B, H,9 0 -1 1 0 -1 S 2S 3S S 2S 3S lag -2σ b) tidsrekke med ikke-stasjonære sesongsvingninger og signifikante autokorrelasjoner utenom sesonglengden Figur 10 Teoretisk form på autokorrelasjonsfunksjonen for ikke-stasjonære tidsrekker. Spesielle tilfeller 2σ lag -2σ Autukorrelasjonsfunksjonen 0.8 0.6 0.4 0.2 0 2σ -0.2 -2σ -0.4 0 5 10 15 20 25 30 35 40 45 50 Avstand mellom observasjonene Figur 11 Autokorrelasjonsfunksjonen for ln-transformerte verdier av mottatte bestillinger, januar 1984 – desember 1991. Region Oslo Autukorrelasjonsfunksjonen 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 0 5 10 15 20 25 30 35 40 45 50 Avstand mellom observasjonene Figur 12 Autokorrelasjonsfunksjonen for lntransformerte verdier av mottatte bestillinger, januar 1984 – desember 1991. Region Oslo. Differensiert en gang 2σ -2σ 115
Page 2 and 3:
Innhold TEMA: Introduksjon, Kjell S
Page 5 and 6:
1 Utvikling av prognosearbeidet i T
Page 7 and 8:
- Prognoser for vanlig telefonabonn
Page 9 and 10:
De økonomiske beregninger som ligg
Page 11 and 12:
ment fra bedrifter. I tillegg er de
Page 13 and 14:
Tele-hjemmearbeid Kommunikasjon mel
Page 15 and 16:
observasjoner, fordi det er en ny t
Page 17 and 18:
1.nyttårsdag (x 10 000) 400 350 30
Page 19 and 20:
20 dere med antall abonnenter. niv
Page 21 and 22:
Indeks 220 200 180 160 140 120 100
Page 23 and 24:
menes at det statistisk ikke er tro
Page 25 and 26:
klassiske prognosemetoden i den fø
Page 27 and 28:
Tabell 6.3 Tidsrekker med forskjell
Page 29 and 30:
38 7.3 Enkel modellbygging Utgangsp
Page 31 and 32:
Når vi bruker minste kvadraters me
Page 33 and 34:
e t 0 99.9 Figur 7.13 Plott av resi
Page 35 and 36:
58 53 48 43 38 33 28 1 0.5 0 -0.5 -
Page 37 and 38:
sjonene eller utviklingen til y. Va
Page 39 and 40:
det kommunisere med. Dermed blir tj
Page 41 and 42:
1 og ved t med (1 - b) og summerer
Page 43 and 44:
i etterspørselen i påfølgende m
Page 45 and 46:
aggregerte prognosen er riktig. Ned
Page 47 and 48:
prognosene vil med sikkerhet ikke v
Page 49 and 50:
skyld, er lite, vil det også være
Page 51:
Ed: O D Anderson. Amsterdam, North
Page 54 and 55:
54 Diverse enkeltpersoner 16 Televe
Page 56 and 57:
Figur 3.3 Innhenting av informasjon
Page 58 and 59:
58 Selvbetjening over telenettet Tj
Page 60 and 61:
60 Det kan være vanskelig med noen
Page 62 and 63:
62 I TITAN-prosjektet ble det foret
Page 64 and 65: 64 Prosentandel av husstander 25 20
Page 66 and 67: 66 I N E T T E T Annullerte bestill
Page 68 and 69: (x 100) 22 17 12 68 7 2 -3 01/87 +
Page 70 and 71: periodene, skyldes at dette skjules
Page 72 and 73: 72 “givende” sentralen til den
Page 74 and 75: 74 spesielt er opptatt av forklarin
Page 76 and 77: 001.18:621.39 76 Glattingsmodeller
Page 78 and 79: 78 Tabell 2 De opprinnelige sesongo
Page 80 and 81: 80 0.025 0.02 0.015 0.01 0.005 y' t
Page 82 and 83: Tabell 3 Holts metode 82 År t Anta
Page 84 and 85: Tabell 5 Hvordan Holt-Winters addit
Page 86 and 87: (x 100) 20 15 10 86 5 0 antall abon
Page 88 and 89: Abonnement 540 520 500 480 460 88 n
Page 90 and 91: 90 ingsprosedyre som skal iterere s
Page 92 and 93: 92 forbedringer av modellen. Plott
Page 94 and 95: 94 Vi ser av (5.12) at variansen ti
Page 96 and 97: 96 Figur 7.2 Residualer fra lineær
Page 98 and 99: 98 Tabellen viser at alle parameter
Page 100 and 101: disse til å lage prognoser med. So
Page 102 and 103: 102 16 Bøe, J, Stordahl, K. Teller
Page 104 and 105: 200 180 160 140 120 100 80 60 40 Fi
Page 106 and 107: 106 1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0
Page 108 and 109: 108 Tabell 2 viser de historiske da
Page 110 and 111: 001.18:621.39 110 Box-Jenkins metod
Page 112 and 113: Standardavvik 600 550 500 450 400 S
Page 116 and 117: 116 Figur 13 Autokorrelasjonsfunksj
Page 118 and 119: 118 Korrelasjonsverdi Vi ser av fig
Page 120 and 121: 120 Aksepter hypotesen om at parame
Page 122 and 123: Residualer 0.4 0.3 0.2 0.1 122 0 -0
Page 124 and 125: 124 Referanser 1 Stordahl, K, Hjelk
Page 126 and 127: Tabell 1 Volum tellerskritt, abonne
Page 128 and 129: 128 Tabell 3a Prognose fra modell b
Page 134 and 135: 001.18:621.39 134 Prognoser for abo
Page 136 and 137: 136 Tabell 3 Analyse av støyledden
Page 138 and 139: 138 Tabell 5 Utskrift av prognosepr
Page 140 and 141: vi ikke diskutere her. Poenget er
Page 142 and 143: 142 prognosen. Da “beskjæres”
Page 144 and 145: 144 7 Stordahl, K. Prognosemetoder:
Page 146 and 147: Tabell 1 Oversikt over takstklassen
Page 148 and 149: 148 Tabell 5 Antall samtalesekunder
Page 150 and 151: 150 a) (x1000) 45 35 25 15 5 (x1000
Page 152 and 153: 152 Tabell 8 viser de avleste telle
Page 154 and 155: 154 Tabell 11 Komplett datasett med
Page 156 and 157: 001.18:621.39 156 Prognoser for nye
Page 158 and 159: 158 3.1 Vurderinger av foreliggende
Page 160 and 161: 160 passer utmerket, med relativt l
Page 162 and 163: 2B+D aksesser (x1000) 7 6 5 4 3 2 1
Page 164 and 165:
164 (x1000) 10 8 6 4 2 0 Tabell 6 I
Page 166 and 167:
001.18:621.39 166 Prognoser for pri
Page 168 and 169:
168 der ˆσ β* = ˆσ = ˆy t =
Page 170 and 171:
n r (t) 90 % 10 170 1,00 0,80 0,60
Page 172 and 173:
ønsker å benytte disse metodene f
Page 174 and 175:
174 Remote router/ Bridge hand, the
Page 176 and 177:
176 Figure 5 ATM cell Bridge 48 byt
Page 178 and 179:
178 DTE less than 2 Mbit/s, Frame R
Page 180 and 181:
180 References 1 Mannsåker, B et a
Page 182 and 183:
182 Table of contents page Introduc
Page 184 and 185:
006 621.391 184 Signal processing B
Page 186 and 187:
006:681.324 006:681.327.8 186 Data
Page 188 and 189:
006 621.39 188 Teletraffic and dime
Page 190 and 191:
190 contractor. The project had a b
Page 192 and 193:
Table 2 ITU Recommendations for con
Page 194 and 195:
006 654.01:65 194 Telecommunication
Page 196 and 197:
006 196 Introduction EURESCOM is an
Page 198:
198 Intelligent networks 26 % Infra
show all

Prognosemetoder – en oversikt - Telenor

Create successful ePaper yourself

Delete template?

Save as template?