Prognosemetoder – en oversikt - Telenor

More documents

Recommendations

Info

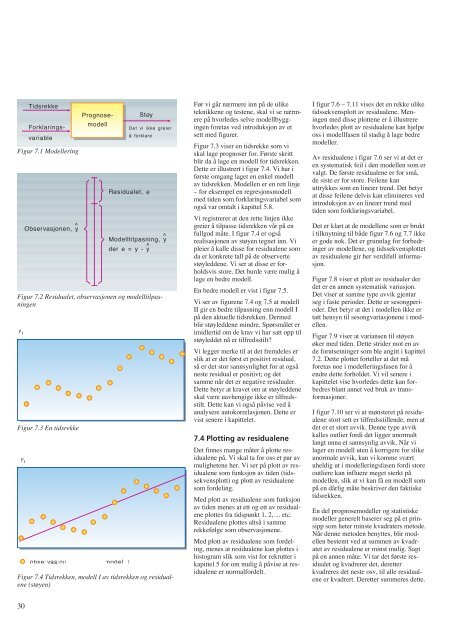
30 Tidsrekke Forklaringsvariable Figur 7.1 Modellering ^ Observasjonen, y Prognosemodell Støy Det vi ikke greier å forklare Residualet, e ^ Modelltilpasning, y ^ der e = y - y Figur 7.2 Residualet, observasjonen og modelltilpasningen y t Figur 7.3 En tidsrekke y t observasjon modell I Figur 7.4 Tidsrekken, modell I av tidsrekken og residualene (støyen) t Før vi går nærmere inn på de ulike teknikkene og testene, skal vi se nærmere på hvorledes selve modellbyggingen foretas ved introduksjon av et sett med figurer. Figur 7.3 viser en tidsrekke som vi skal lage prognoser for. Første skritt blir da å lage en modell for tidsrekken. Dette er illustrert i figur 7.4. Vi har i første omgang laget en enkel modell av tidsrekken. Modellen er en rett linje – for eksempel en regresjonsmodell med tiden som forklaringsvariabel som også var omtalt i kapittel 5.8. Vi registrerer at den rette linjen ikke greier å tilpasse tidsrekken vår på en fullgod måte. I figur 7.4 er også realisasjonen av støyen tegnet inn. Vi pleier å kalle disse for residualene som da er konkrete tall på de observerte støyleddene. Vi ser at disse er forholdsvis store. Det burde være mulig å lage en bedre modell. En bedre modell er vist i figur 7.5. Vi ser av figurene 7.4 og 7.5 at modell II gir en bedre tilpasning enn modell I på den aktuelle tidsrekken. Dermed blir støyleddene mindre. Spørsmålet er imidlertid om de krav vi har satt opp til støyleddet nå er tilfredsstilt? Vi legger merke til at det fremdeles er slik at er det først et positivt residual, så er det stor sannsynlighet for at også neste residual er positivt; og det samme når det er negative residualer. Dette betyr at kravet om at støyleddene skal være uavhengige ikke er tilfredsstilt. Dette kan vi også påvise ved å analysere autokorrelasjonen. Dette er vist senere i kapittelet. 7.4 Plotting av residualene Det finnes mange måter å plotte residualene på. Vi skal ta for oss et par av mulighetene her. Vi ser på plott av residualene som funksjon av tiden (tidssekvensplott) og plott av residualene som fordeling. Med plott av residualene som funksjon av tiden menes at ett og ett av residualene plottes fra tidspunkt 1, 2, ... etc. Residualene plottes altså i samme rekkefølge som observasjonene. Med plott av residualene som fordeling, menes at residualene kan plottes i histogram slik som vist for rekrutter i kapittel 5 for om mulig å påvise at residualene er normalfordelt. I figur 7.6 – 7.11 vises det en rekke ulike tidssekvensplott av residualene. Meningen med disse plottene er å illustrere hvorledes plott av residualene kan hjelpe oss i modellfasen til stadig å lage bedre modeller. Av residualene i figur 7.6 ser vi at det er en systematisk feil i den modellen som er valgt. De første residualene er for små, de siste er for store. Feilene kan uttrykkes som en lineær trend. Det betyr at disse feilene delvis kan elimineres ved introduksjon av en lineær trend med tiden som forklaringsvariabel. Det er klart at de modellene som er brukt i tilknytning til både figur 7.6 og 7.7 ikke er gode nok. Det er grunnlag for forbedringer av modellene, og tidssekvensplottet av residualene gir her verdifull informasjon. Figur 7.8 viser et plott av residualer der det er en annen systematisk variasjon. Det viser at samme type avvik gjentar seg i faste perioder. Dette er sesongperioder. Det betyr at det i modellen ikke er tatt hensyn til sesongvariasjonene i modellen. Figur 7.9 viser at variansen til støyen øker med tiden. Dette strider mot en av de forutsetninger som ble angitt i kapittel 7.2. Dette plottet forteller at det må foretas noe i modelleringsfasen for å endre dette forholdet. Vi vil senere i kapittelet vise hvorledes dette kan forbedres blant annet ved bruk av transformasjoner. I figur 7.10 ser vi at mønsteret på residualene stort sett er tilfredsstillende, men at det er et stort avvik. Denne type avvik kalles outlier fordi det ligger unormalt langt unna et sannsynlig avvik. Når vi lager en modell uten å korrigere for slike unormale avvik, kan vi komme svært uheldig ut i modelleringsfasen fordi store outliere kan influere meget sterkt på modellen, slik at vi kan få en modell som på en dårlig måte beskriver den faktiske tidsrekken. En del prognosemodeller og statistiske modeller generelt baserer seg på et prinsipp som heter minste kvadraters metode. Når denne metoden benyttes, blir modellen bestemt ved at summen av kvadratet av residualene er minst mulig. Sagt på en annen måte: Vi tar det første residualet og kvadrerer det, deretter kvadreres det neste osv, til alle residualene er kvadrert. Deretter summeres dette.
Når vi bruker minste kvadraters metode bestemmes modellen ut fra at summen av kvadratet av residualene er minst mulig. Når vi bruker denne type metoder er det derfor viktig gå nøye igjennom residualene for å undersøke om det forekommer outliere fordi disse vil påvirke modellen i sterk grad. Dette skyldes at når selve residualet er stort, vil kvadratet av residualet bli dominerende og dermed tvinge fram en modell som gir en dårlig beskrivelse av tidsrekken. Dette er illustrert i figur 7.11 og 7.12. Vi må derfor være varsomme når vi oppdager spesielt store avvik i residualene. I første omgang bør det stilles spørsmål om hvorfor de er så store. Det kan skyldes feilmålinger, annen type registreringsfeil, eventuelle misforståelser/ kommunikasjonssvikt, innleggingsfeil av data, etc. I slike tilfeller må dataene rettes slik at de blir korrekte. En outlier kan også skyldes spesielt oppståtte, men unormale situasjoner. Det kan eksempelvis bli registrert lav etterspørsel på grunn av en streik e l. I slike tilfeller er dataene korrekte, men de gir ikke noe representativt bilde av situasjonen. Det vil ikke være riktig å bruke denne observasjonen som grunnlag for videre prognostisering når det ikke vil være noen streik de kommende perioder. Dersom vi imidlertid vet at det kommer en streik, må vi selvsagt ta hensyn til det i prognosene. I figur 7.11 og 7.12 er det vist hvorledes en stor outlier påvirker modellen og dermed også prognosene. Vi har i figur 7.11 en enkel regresjonsmodell med tiden som forklaringsvariabel og hvor det er en spesielt stor outlier i begynnelsen av observasjonene. Vi har i figuren foretatt en modelltilpasning uten at det er korrigert for outlieren. I figur 7.12 har vi de samme observasjonene, men her er det korrigert for outlieren, noe som må gjøres under modellbyggingen. Vi ser nå at vi får en helt annen modell og dermed også helt andre prognoser. I noen tilfeller kan vi klart se at vi har en outlier fordi den ligger svært langt borte fra det som er normalt. I andre tilfeller kan det være vanskeligere å avgjøre om vi har en outlier eller ikke. Noen programpakker framstiller tidssekvensplottet av residualene med et usikkerhetsintervall som er lik to ganger standardavviket til residualene. Dette er vist i figur 7.13. I kapittel 5.6.2 ble egenskaper til normalfordelingen gjennomgått. Vanligvis vil støyen (residualene) tilnærmet tilfreds- stille en normalfordeling. Da vil omlag 5 % av residualene ligge utenfor to ganger standardaviket, mens kun 0,3 % av residualene vil ligge utenfor tre ganger standardavviket. Dette betyr at dersom ett av residualene avviker i størrelsesorden tre ganger standardavviket eller mer, er det grunn til å stille spørsmålstegn ved den observasjonen som har generert residualet. Denne må karakteriseres som en outlier. Det siste som bør ses på, er i hvilken grad residualene tilfredsstiller normalfordelingen. Dette kan gjøres på flere måter. I noen programpakker er det lagt inn et spesielt normalfordelingsplott. Dette kan da benyttes. Plottet gjøres på en spesiell form slik at når residualene ordnes i stigende rekkefølge skal de tilnærmet ligge på en rett linje. Skalaen i plottet er transformert slik som vist i figur 7.14. Det er også mulig å plotte residualene slik som vist i figur 5.2 for å få et inntrykk av fordelingen til residualene. Det anbefales imidlertid å benytte et normalfordelingsplott dersom dette er tilgjengelig i programpakken. Det bør også sies at forutsetningen om normalfordelte støyledd ikke er det mest kritiske. Det er fullt mulig å foreta mesteparten av modellbyggingen uten forutsetning om at støyleddene er normalfordelte. Vi har nå vært igjennom en del ulike mønstre som vi kan ha på plottet av residualene. Vi forstår nå hvor viktig det er å foreta slike plott etter at vi har laget en modell. Figur 7.1 beskriver nettopp dette. På grunnlag av dataene lager vi en modell, deretter sammenlikner vi observasjonene i tidsrekken med de tilpassede dataene fra modelleringen. Differansen mellom disse er residualene som så plottes ut. Dersom disse ikke tilfredsstiller de krav som er gitt i kapittel 7.2 for støyen, må vi prøve å finne fram til en bedre modell. Selv om vi ennå ikke har beskrevet de aktuelle prognosemetodene, har vi så langt fått et godt grunnlag for hvorledes det må arbeides med modellbyggingen for å få fram gode prognosemodeller. Det som vi skal stå tilbake med til slutt er et residualplott slik som vist i figur 7.15, der residualene er tilfeldig e t 0 e t 0 e t 0 y t observasjon modell II Figur 7.5 Tidsrekke, modell II av tidsrekken og residualene (støyen) Figur 7.6 Plott av residualer fra en modell som bør ha en trend Figur 7.7 Plott av residualer fra en modell som gir dårlig tilpasning Figur 7.8 Plott av residualer fra en modell som ikke har bygget inn sesongvariasjoner t 31
Page 2 and 3: Innhold TEMA: Introduksjon, Kjell S
Page 5 and 6: 1 Utvikling av prognosearbeidet i T
Page 7 and 8: - Prognoser for vanlig telefonabonn
Page 9 and 10: De økonomiske beregninger som ligg
Page 11 and 12: ment fra bedrifter. I tillegg er de
Page 13 and 14: Tele-hjemmearbeid Kommunikasjon mel
Page 15 and 16: observasjoner, fordi det er en ny t
Page 17 and 18: 1.nyttårsdag (x 10 000) 400 350 30
Page 19 and 20: 20 dere med antall abonnenter. niv
Page 21 and 22: Indeks 220 200 180 160 140 120 100
Page 23 and 24: menes at det statistisk ikke er tro
Page 25 and 26: klassiske prognosemetoden i den fø
Page 27 and 28: Tabell 6.3 Tidsrekker med forskjell
Page 29: 38 7.3 Enkel modellbygging Utgangsp
Page 33 and 34: e t 0 99.9 Figur 7.13 Plott av resi
Page 35 and 36: 58 53 48 43 38 33 28 1 0.5 0 -0.5 -
Page 37 and 38: sjonene eller utviklingen til y. Va
Page 39 and 40: det kommunisere med. Dermed blir tj
Page 41 and 42: 1 og ved t med (1 - b) og summerer
Page 43 and 44: i etterspørselen i påfølgende m
Page 45 and 46: aggregerte prognosen er riktig. Ned
Page 47 and 48: prognosene vil med sikkerhet ikke v
Page 49 and 50: skyld, er lite, vil det også være
Page 51: Ed: O D Anderson. Amsterdam, North
Page 54 and 55: 54 Diverse enkeltpersoner 16 Televe
Page 56 and 57: Figur 3.3 Innhenting av informasjon
Page 58 and 59: 58 Selvbetjening over telenettet Tj
Page 60 and 61: 60 Det kan være vanskelig med noen
Page 62 and 63: 62 I TITAN-prosjektet ble det foret
Page 64 and 65: 64 Prosentandel av husstander 25 20
Page 66 and 67: 66 I N E T T E T Annullerte bestill
Page 68 and 69: (x 100) 22 17 12 68 7 2 -3 01/87 +
Page 70 and 71: periodene, skyldes at dette skjules
Page 72 and 73: 72 “givende” sentralen til den
Page 74 and 75: 74 spesielt er opptatt av forklarin
Page 76 and 77: 001.18:621.39 76 Glattingsmodeller
Page 78 and 79: 78 Tabell 2 De opprinnelige sesongo
Page 80 and 81:
80 0.025 0.02 0.015 0.01 0.005 y' t
Page 82 and 83:
Tabell 3 Holts metode 82 År t Anta
Page 84 and 85:
Tabell 5 Hvordan Holt-Winters addit
Page 86 and 87:
(x 100) 20 15 10 86 5 0 antall abon
Page 88 and 89:
Abonnement 540 520 500 480 460 88 n
Page 90 and 91:
90 ingsprosedyre som skal iterere s
Page 92 and 93:
92 forbedringer av modellen. Plott
Page 94 and 95:
94 Vi ser av (5.12) at variansen ti
Page 96 and 97:
96 Figur 7.2 Residualer fra lineær
Page 98 and 99:
98 Tabellen viser at alle parameter
Page 100 and 101:
disse til å lage prognoser med. So
Page 102 and 103:
102 16 Bøe, J, Stordahl, K. Teller
Page 104 and 105:
200 180 160 140 120 100 80 60 40 Fi
Page 106 and 107:
106 1 0.8 0.6 0.4 0.2 0 1 0.8 0.6 0
Page 108 and 109:
108 Tabell 2 viser de historiske da
Page 110 and 111:
001.18:621.39 110 Box-Jenkins metod
Page 112 and 113:
Standardavvik 600 550 500 450 400 S
Page 114 and 115:
114 AR-parametre og q MA-parametre
Page 116 and 117:
116 Figur 13 Autokorrelasjonsfunksj
Page 118 and 119:
118 Korrelasjonsverdi Vi ser av fig
Page 120 and 121:
120 Aksepter hypotesen om at parame
Page 122 and 123:
Residualer 0.4 0.3 0.2 0.1 122 0 -0
Page 124 and 125:
124 Referanser 1 Stordahl, K, Hjelk
Page 126 and 127:
Tabell 1 Volum tellerskritt, abonne
Page 128 and 129:
128 Tabell 3a Prognose fra modell b
Page 130 and 131:
Page 132 and 133:
Page 134 and 135:
001.18:621.39 134 Prognoser for abo
Page 136 and 137:
136 Tabell 3 Analyse av støyledden
Page 138 and 139:
138 Tabell 5 Utskrift av prognosepr
Page 140 and 141:
vi ikke diskutere her. Poenget er
Page 142 and 143:
142 prognosen. Da “beskjæres”
Page 144 and 145:
144 7 Stordahl, K. Prognosemetoder:
Page 146 and 147:
Tabell 1 Oversikt over takstklassen
Page 148 and 149:
148 Tabell 5 Antall samtalesekunder
Page 150 and 151:
150 a) (x1000) 45 35 25 15 5 (x1000
Page 152 and 153:
152 Tabell 8 viser de avleste telle
Page 154 and 155:
154 Tabell 11 Komplett datasett med
Page 156 and 157:
001.18:621.39 156 Prognoser for nye
Page 158 and 159:
158 3.1 Vurderinger av foreliggende
Page 160 and 161:
160 passer utmerket, med relativt l
Page 162 and 163:
2B+D aksesser (x1000) 7 6 5 4 3 2 1
Page 164 and 165:
164 (x1000) 10 8 6 4 2 0 Tabell 6 I
Page 166 and 167:
001.18:621.39 166 Prognoser for pri
Page 168 and 169:
168 der ˆσ β* = ˆσ = ˆy t =
Page 170 and 171:
n r (t) 90 % 10 170 1,00 0,80 0,60
Page 172 and 173:
ønsker å benytte disse metodene f
Page 174 and 175:
174 Remote router/ Bridge hand, the
Page 176 and 177:
176 Figure 5 ATM cell Bridge 48 byt
Page 178 and 179:
178 DTE less than 2 Mbit/s, Frame R
Page 180 and 181:
180 References 1 Mannsåker, B et a
Page 182 and 183:
182 Table of contents page Introduc
Page 184 and 185:
006 621.391 184 Signal processing B
Page 186 and 187:
006:681.324 006:681.327.8 186 Data
Page 188 and 189:
006 621.39 188 Teletraffic and dime
Page 190 and 191:
190 contractor. The project had a b
Page 192 and 193:
Table 2 ITU Recommendations for con
Page 194 and 195:
006 654.01:65 194 Telecommunication
Page 196 and 197:
006 196 Introduction EURESCOM is an
Page 198:
198 Intelligent networks 26 % Infra
show all

Prognosemetoder – en oversikt - Telenor

Create successful ePaper yourself

Delete template?

Save as template?