Prognosemetoder – en oversikt - Telenor

angi prognoser for akkumulert produksjonsvolum
ved tidspunkt T. Dette
uttrykket kan så settes inn i Wrights
utvidet lærekurvemodell, og vi får:
(5.3)
Dette uttrykket angir da prisprognose for
nettkomponenter gitt at n er akkumulert
produksjonsvolum.
Hvis vi isteden benytter Crawfords utvidede
lærekurvemodell der er
definert som antall enheter produsert i en
serie ved tidspunkt t, vil vi få andre
formler for prisprognosen.
La igjen
n(1), n(2), ..., n(s)
være det akkumulerte produksjonsvolum.
Da vil:
n*(t) = n(t) - n(t-1) (5.4)
Med andre ord, differansen mellom
akkumulert produksjonsvolum ved tidspunkt
t og t-1, angir hvor stort produksjonsvolumet
er ved tidspunkt t. Av
likning (5.4) og likning (5.2) får vi følgende:
ˆn(T )* =
ˆM 1 + e â+ ˆ − ˆg
⎛ bT ⎞
⎜ ⎟ −
⎝ ⎠
ˆ M 1 + e â+ ˆ − ˆg
⎛ b(T −1) ⎞
⎜
⎟
⎝
⎠
ˆn
ˆP n(T ) = ˆα
t *
ˆ M 1 + e â+ ˆ − ˆg
β
ˆ
⎡
⎤
⎢ ⎛ bT ⎞
⎜ ⎟ ⎥
⎢ ⎝ ⎠ ⎥
⎣
⎦
(5.5)
Dette uttrykket settes så inn i Crawfords
utvidede lærekurvemodell og vi får:
ˆP n(T ) =
ˆα
(5.6)
Dette uttrykket angir da prisprognose for
nettkomponenter gitt at n*(t) er produksjonsvolum
pr tidsintervall.
ˆ M 1 + e â+ ˆ − ˆg
⎛ bT ⎞
⎜ ⎟ −
⎝ ⎠
ˆ M 1 + e â+ ˆ ⎡
− ˆg ⎤
⎢
⎛ b(T −1) ⎞
⎜
⎟ ⎥
⎢
⎝
⎠ ⎥
⎣
⎦
6 Praktisk fortolkning av
prognosemodellen
β
ˆ
Vi skal nå vise hvorledes prognosemodellen
kan benyttes for å beskrive pris på
komponenter som funksjon av tiden og
se på betydningen av de parametrene
som inngår.
Spesielt når det dreier seg om nye komponenter
som bare foreligger i form av
prototyper eller hvor produksjonen er
helt i startfasen er det viktig å ha en modell
som en kan analysere og benytte for
å gjøre gode antakelser om prisutvik-
Relativt akkumulert volum
1,00
0,80
0,60
0,40
0,20
lingen. Det er derfor viktig å forstå hva
parametrene betyr i modellen.
En viktig konsekvens som vi kan trekke
av å kombinere en logistisk modell som i
likning (5.1), (hvor vi for enkelhets skyld
setter g = 1 som konstant), med en lærekurve
som i likning (3.1)
Pn(t) = αn(t) β (6.1)
er at det ikke vil være nødvendig å
beskrive n(t) som et globalt akkumulert
volum, men vi kan nøye oss med den
relative prognosen
(6.2)
hvor nr (t) går fra 0 til 1.
Dette betyr at vi f eks kan benytte volumprognoser
i et enkelt land eller i noen
storbyer hvor anvendelsen av komponenten
kan antas å være representativ for
den globale utviklingen. Det betyr at en
ikke trenger informasjonen om det totale
globale produksjonsvolum (eller akkumulert
globalt volum) som det kan være
vanskelig å få data på.
Den relative volumfunksjonen nr (t) kan
skrives (se appendiks):
nr (t )= ( 1 + ea+bt ) −1
n r (0)
0,05
0,10
0,20
0,50
0,90
1,00
0
0 1 2 3 4 5 6 7 8 9 10 år
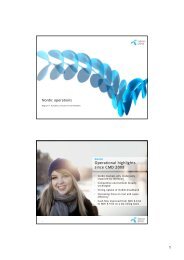
Figur 6.1 Relativt akkumulert volum som funksjon av tiden for en konstant ∆T
= 10 år og med nr (0) varierende fra 0,05 til 1
Relativt akkumulert volum
1,00
0,80
0,60
0,40
0,20
0
0 1 2 3 4 5 6 7 8 9 10 år
Figur 6.2 Økning av relativt akkumulert volum som funksjon av tiden når
nr (0) = 0,01 holdes konstant og ∆T varierer fra 2 til 20 år
∆T
2
4
8
12
16
20
ln(nr(0)
nr (t )= 1 + e
(6.3)
−1−1)− 2ln9
∆T t
−1
⎡ ⎧
⎫ ⎤
⎢ ⎨
⎬
⎩
⎭ ⎥
⎢
⎥
⎢
⎥
⎣
⎦
hvor nr (0) er funksjonsverdien når t =0
og ∆T er den tiden det tar fra funksjonsverdien
nr (t1 ) er 10 % til nr (t2 ) = 90 %,
dvs ∆T = t2 - t1 .
Figur 6.1 viser nå denne relasjonen for
det tilfellet at ∆T = 10 år holdes konstant
og nr (0) varierer fra 5 % til 100 %.
Figur 6.2 viser hvorledes nr (t) utvikler
seg med nr (0) = 0,01 og med ∆T varierende
fra 2 til 20 år.
Parametrene a og b er nå uttrykt ved
nr (0) og ∆T der
a = ln(nr (0) -1 - 1) (6.4)
og
2ln9 b = −
∆T (6.5)
Vi ser at nr (0) (i likhet med a) bestemmer
hvor på tidsaksen kurven skal ligge,
mens ∆T (eller b) forteller om kurven
dekker et langt eller et kort tidsforløp
(dvs fra funksjonsverdien er 10 % til den
≈−4,4
∆T
169