Immersioni aperte in dimensione infinita - Dipartimento di Matematica
Immersioni aperte in dimensione infinita - Dipartimento di Matematica
Immersioni aperte in dimensione infinita - Dipartimento di Matematica
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
60 Embedd<strong>in</strong>g aperti <strong>di</strong> varietà <strong>di</strong> <strong><strong>di</strong>mensione</strong> <strong>in</strong>f<strong>in</strong>ita<br />
ℓn<br />
<br />
Mn × H n<br />
<br />
<br />
∪<br />
D 0 n<br />
<br />
jn<br />
Gn+1<br />
<br />
<br />
<br />
U 0 n+1 × Hn+1 Un+1 × H<br />
<br />
n+1<br />
<br />
∩<br />
<br />
Mn+1 × H n+1<br />
<br />
<br />
∪<br />
D 0 n+1<br />
∩<br />
∩<br />
Jn+1,1 <br />
Mn+1 × Hn+1 <br />
<br />
gn<br />
<br />
<br />
<br />
H<br />
<br />
<br />
gn+1 <br />
d<br />
<br />
<br />
<br />
<br />
−1<br />
<br />
<br />
<br />
1 ◦ ˜g<br />
<br />
<br />
<br />
<br />
H<br />
id<br />
(2.7.14)<br />
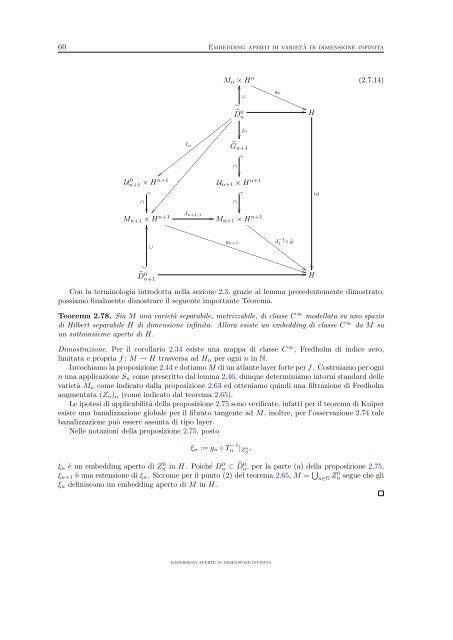
Con la term<strong>in</strong>ologia <strong>in</strong>trodotta nella sezione 2.3, grazie al lemma precedentemente <strong>di</strong>mostrato,<br />
possiamo f<strong>in</strong>almente <strong>di</strong>mostrare il seguente importante Teorema.<br />
Teorema 2.78. Sia M una varietà separabile, metrizzabile, <strong>di</strong> classe C ∞ modellata su uno spazio<br />
<strong>di</strong> Hilbert separabile H <strong>di</strong> <strong><strong>di</strong>mensione</strong> <strong>in</strong>f<strong>in</strong>ita. Allora esiste un embedd<strong>in</strong>g <strong>di</strong> classe C ∞ da M su<br />
un sotto<strong>in</strong>sieme aperto <strong>di</strong> H.<br />
Dimostrazione. Per il corollario 2.34 esiste una mappa <strong>di</strong> classe C ∞ , Fredholm <strong>di</strong> <strong>in</strong><strong>di</strong>ce zero,<br />
limitata e propria f : M → H trasversa ad Hn per ogni n <strong>in</strong> N.<br />
Invochiamo la proposizione 2.44 e dotiamo M <strong>di</strong> un atlante layer forte per f. Costruiamo per ogni<br />
n una applicazione Sn come prescritto dal lemma 2.46, dunque determ<strong>in</strong>iamo <strong>in</strong>torni standard delle<br />
varietà Mn come <strong>in</strong><strong>di</strong>cato dalla proposizione 2.63 ed otteniamo qu<strong>in</strong><strong>di</strong> una filtrazione <strong>di</strong> Fredholm<br />
augmentata (Zn)n (come <strong>in</strong><strong>di</strong>cato dal teorema 2.65).<br />
Le ipotesi <strong>di</strong> applicabilità della proposizione 2.75 sono verificate, <strong>in</strong>fatti per il teorema <strong>di</strong> Kuiper<br />
esiste una banalizzazione globale per il fibrato tangente ad M, <strong>in</strong>oltre, per l’osservazione 2.74 tale<br />
banalizzazione può essere assunta <strong>di</strong> tipo layer.<br />
Nelle notazioni della proposizione 2.75, posto<br />
ξn := gn ◦ T −1<br />
n | Z 0 n ,<br />
ξn è un embedd<strong>in</strong>g aperto <strong>di</strong> Z 0 n <strong>in</strong> H. Poiché D 0 n ⊂ D 0 n, per la parte (a) della proposizione 2.75,<br />
ξn+1 è una estensione <strong>di</strong> ξn. Siccome per il punto (2) del teorema 2.65, M = <br />
n∈N Z0 n segue che gli<br />
ξn def<strong>in</strong>iscono un embedd<strong>in</strong>g aperto <strong>di</strong> M <strong>in</strong> H.<br />
IMMERSIONI APERTE IN DIMENSIONE INFINITA