Apunte

94 5. INTERPOLACI ÓN
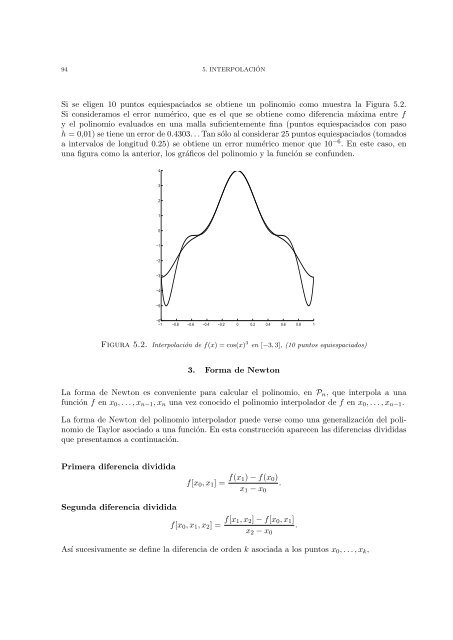
Si se eligen 10 puntos equiespaciados se obtiene un polinomio como muestra la Figura 5.2.
Si consideramos el error numérico, que es el que se obtiene como diferencia máxima entre f
y el polinomio evaluados en una malla suficientemente fina (puntos equiespaciados con paso
h = 0,01) se tiene un error de 0.4303. . . Tan sólo al considerar 25 puntos equiespaciados (tomados
a intervalos de longitud 0.25) se obtiene un error numérico menor que 10 −6 . En este caso, en
una figura como la anterior, los gráficos del polinomio y la función se confunden.
4
3
2
1
0
−1
−2
−3
−4
−5
−6
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
Figura 5.2. Interpolación de f(x) = cos(x) 3 en [−3, 3], (10 puntos equiespaciados)
3. Forma de Newton
La forma de Newton es conveniente para calcular el polinomio, en Pn, que interpola a una
función f en x0, . . . , xn−1, xn una vez conocido el polinomio interpolador de f en x0, . . . , xn−1.
La forma de Newton del polinomio interpolador puede verse como una generalización del polinomio
de Taylor asociado a una función. En esta construcción aparecen las diferencias divididas
que presentamos a continuación.
Primera diferencia dividida
Segunda diferencia dividida
f[x0, x1] = f(x1) − f(x0)
.
x1 − x0
f[x0, x1, x2] = f[x1, x2] − f[x0, x1]
.
x2 − x0
Así sucesivamente se define la diferencia de orden k asociada a los puntos x0, . . . , xk,