TH`ESE DE DOCTORAT DE L'UNIVERSITÉ PARIS 6 Spécialité ...

58 Robustesse de la formation de faisceaux bande étroite par rapport à la largeur de bande
300
250
200
a(f,m)
150
100
50
0
−0.5 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5
f/B
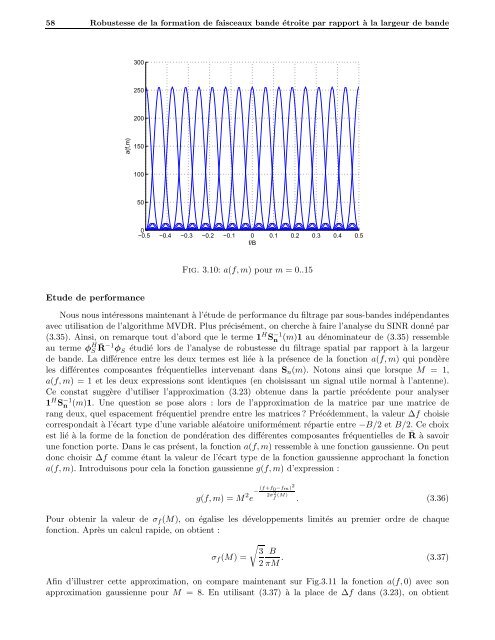
Fig. 3.10: a(f,m) pour m = 0..15
Etude de performance
Nous nous intéressons maintenant à l’étude de performance du filtrage par sous-bandes indépendantes
avec utilisation de l’algorithme MVDR. Plus précisément, on cherche à faire l’analyse du SINR donné par
(3.35). Ainsi, on remarque tout d’abord que le terme 1 H S −1
n (m)1 au dénominateur de (3.35) ressemble
au terme φ H ¯R S −1 φ S étudié lors de l’analyse de robustesse du filtrage spatial par rapport à la largeur
de bande. La différence entre les deux termes est liée à la présence de la fonction a(f,m) qui pondère
les différentes composantes fréquentielles intervenant dans S n (m). Notons ainsi que lorsque M = 1,
a(f,m) = 1 et les deux expressions sont identiques (en choisissant un signal utile normal à l’antenne).
Ce constat suggère d’utiliser l’approximation (3.23) obtenue dans la partie précédente pour analyser
1 H S −1
n (m)1. Une question se pose alors : lors de l’approximation de la matrice par une matrice de
rang deux, quel espacement fréquentiel prendre entre les matrices Précédemment, la valeur ∆f choisie
correspondait à l’écart type d’une variable aléatoire uniformément répartie entre −B/2 et B/2. Ce choix
est lié à la forme de la fonction de pondération des différentes composantes fréquentielles de ¯R à savoir
une fonction porte. Dans le cas présent, la fonction a(f,m) ressemble à une fonction gaussienne. On peut
donc choisir ∆f comme étant la valeur de l’écart type de la fonction gaussienne approchant la fonction
a(f,m). Introduisons pour cela la fonction gaussienne g(f,m) d’expression :
g(f,m) = M 2 e −(f+f 0 −fm)2
2σ 2 f (M) . (3.36)
Pour obtenir la valeur de σ f (M), on égalise les développements limités au premier ordre de chaque
fonction. Après un calcul rapide, on obtient :
σ f (M) =
√
3
2
B
πM . (3.37)
Afin d’illustrer cette approximation, on compare maintenant sur Fig.3.11 la fonction a(f,0) avec son
approximation gaussienne pour M = 8. En utilisant (3.37) à la place de ∆f dans (3.23), on obtient