TH`ESE DE DOCTORAT DE L'UNIVERSITÉ PARIS 6 Spécialité ...

60 Robustesse de la formation de faisceaux bande étroite par rapport à la largeur de bande
2.5
2
1.5
SINR (dB)
1
0.5
0
−0.5
exact, a(f,m)
approximation
exact, a(f,m)=g(f,m)
−1
0 10 20 30 40 50 60 70
M
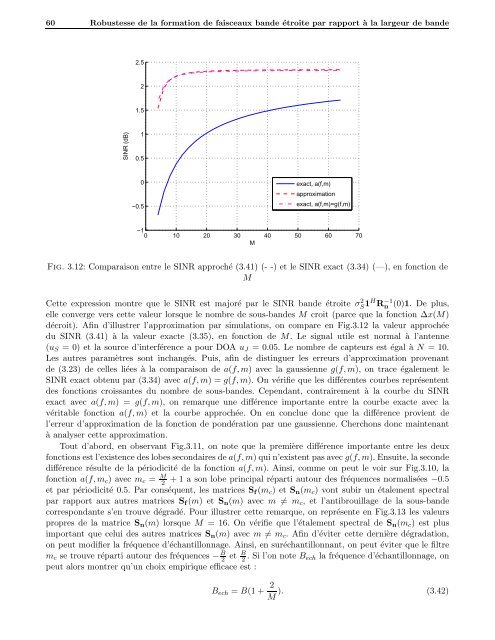
Fig. 3.12: Comparaison entre le SINR approché (3.41) (- -) et le SINR exact (3.34) (—), en fonction de
M
Cette expression montre que le SINR est majoré par le SINR bande étroite σS 21H R −1
n (0)1. De plus,
elle converge vers cette valeur lorsque le nombre de sous-bandes M croit (parce que la fonction ∆x(M)
décroit). Afin d’illustrer l’approximation par simulations, on compare en Fig.3.12 la valeur approchée
du SINR (3.41) à la valeur exacte (3.35), en fonction de M. Le signal utile est normal à l’antenne
(u S = 0) et la source d’interférence a pour DOA u J = 0.05. Le nombre de capteurs est égal à N = 10.
Les autres paramètres sont inchangés. Puis, afin de distinguer les erreurs d’approximation provenant
de (3.23) de celles liées à la comparaison de a(f,m) avec la gaussienne g(f,m), on trace également le
SINR exact obtenu par (3.34) avec a(f,m) = g(f,m). On vérifie que les différentes courbes représentent
des fonctions croissantes du nombre de sous-bandes. Cependant, contrairement à la courbe du SINR
exact avec a(f,m) = g(f,m), on remarque une différence importante entre la courbe exacte avec la
véritable fonction a(f,m) et la courbe approchée. On en conclue donc que la différence provient de
l’erreur d’approximation de la fonction de pondération par une gaussienne. Cherchons donc maintenant
à analyser cette approximation.
Tout d’abord, en observant Fig.3.11, on note que la première différence importante entre les deux
fonctions est l’existence des lobes secondaires de a(f,m) qui n’existent pas avec g(f,m). Ensuite, la seconde
différence résulte de la périodicité de la fonction a(f,m). Ainsi, comme on peut le voir sur Fig.3.10, la
fonction a(f,m c ) avec m c = M 2
+ 1 a son lobe principal réparti autour des fréquences normalisées −0.5
et par périodicité 0.5. Par conséquent, les matrices S f (m c ) et S n (m c ) vont subir un étalement spectral
par rapport aux autres matrices S f (m) et S n (m) avec m ≠ m c , et l’antibrouillage de la sous-bande
correspondante s’en trouve dégradé. Pour illustrer cette remarque, on représente en Fig.3.13 les valeurs
propres de la matrice S n (m) lorsque M = 16. On vérifie que l’étalement spectral de S n (m c ) est plus
important que celui des autres matrices S n (m) avec m ≠ m c . Afin d’éviter cette dernière dégradation,
on peut modifier la fréquence d’échantillonnage. Ainsi, en suréchantillonnant, on peut éviter que le filtre
m c se trouve réparti autour des fréquences − B 2 et B 2 . Si l’on note B ech la fréquence d’échantillonnage, on
peut alors montrer qu’un choix empirique efficace est :
B ech = B(1 + 2 ). (3.42)
M