Modern Engineering Thermodynamics

More documents

Recommendations

Info

13.7 Rankine Cycle with Regeneration 473 pressure), and pump 2 brings the pressure the rest of the way up from 80.0 to 200. psia. Then, v 3 = v f (1.00 psia) = 0.01614 ft 3 /lbm and v 6 = v f (80.0 psia) = 0.01757 ft 3 /lbm. The additional monitoring station data needed are Station 4s p 4s = p 4 = 80:0 psia s 4s = s 3 = 0:1326 Btu/ðlbm . RÞ Station 5s p 5s = p 4 = 80:0 psia h 4s = h 3 + v 3 ðp 4 – p 3 Þ x 5s = 0:9358 s 5s = s 1 = 1:5466 Btu/ðlbm . RÞ = 69:7 + ð0:01614Þð80:0 – 1:00Þð144/778:16Þ h 5s = 1125:7 Btu/lbm = 69:7 + 0:236 = 69:9 Btu/lbm Station 6 p 6 = 80:0 psia x 6 = 0:00 Station 7s p 7s = p 7 = 200: psia s 7s = s 6 = 0:4535 Btu/ðlbm . RÞ h 6 = 282:2 Btu/lbm h 7s = h 6 + v 6 ðp 7 – p 6 Þ s 6 = 0:4535 Btu/ðlbm . RÞ = 282:2 + ð0:01757Þð200: – 80:0Þð144/778Þ = 282:2 + 0:390 = 282:6 Btu/lbm where, at station 5s, wedeterminethatx 5s = (1.5466 – 0.4535)/1.1681 = 0.9358 and h 5s = 282.2 + (0.9358)(901.4) = 1125.7 Btu/lbm. Equation (13.11) now gives the value of y as y = h 6 − h 4s 282:6 − 69:9 = h 5s − h 4s 1125:7 − 69:9 = 0:201 then, the isentropic thermal efficiency of the cycle is given by Eq. (13.12b) with all the η s = 1.0 as ðη T Þ Rankine cycle = 1 − h 2s − h 3 ð1 − yÞ = 1 − 863:5 − 69:7 ð1 − 0:201Þ = 0:308 = 30:8% h 1 − h 7s 1199:3 − 282:6 with 1 regenerator By altering the value of y (the amount of steam bled from the turbine) and recomputing the value of h 7s , it becomes clear that the cycle thermal efficiency is maximized at 31.2% when y = 0.138. This is shown in Figure 13.23. 32.0 0.30 Cycle thermal efficiency Cycle thermal efficiency (%) 31.0 30.0 Regenerator mass fraction 0.20 0.10 Regenerator mass fraction, y FIGURE 13.23 Example 13.6, plot of solution. 29.0 0 40 80 120 160 200 0.00 Regenerator pressure, psia Exercises 16. The operator of the plant described in Example 13.6 changes the boiler outlet state from dry saturated steam at 200. psia to dry saturated steam at 400. psia. Determine the mass fraction of regeneration steam that is now required to produce saturated liquid water at 80.0 psia at the end of the open loop regenerator. Assume all the other variables remain unchanged. Answer: y = 0.210 17. If the interstage steam pressure in Example 13.6 is increased from 80.0 to 150. psia, determine the new isentropic Rankine cycle thermal efficiency. Assume all the other variables remain unchanged. Answer: (η T ) isentropic Rankine = 31.0%. 18. The power plant engineer mentioned in Exercise 16 just informed us that the first and second stage prime mover isentropic efficiencies are 75.0% and 68.0%, respectively, and that the boiler feed pump isentropic efficiency is 83.0%. Now determine the actual Rankine cycle thermal efficiency of this system with the 80.0 psia open loop regenerator. Answer: (η T ) Rankine = 25.8%.
474 CHAPTER 13: Vapor and Gas Power Cycles Note that the effect of a single regeneration unit in the previous example was to increase the thermal efficiency by only 1.1%. The extra expense of the regenerators and the additional pumps cannot be economically justified unless the system is large enough to make such a small thermal efficiency increment produces a significant savings in fuel costs. This type of Rankine cycle regeneration was first seriously proposed in 1890 and first implemented in 1898 with a four-stage, quadruple-expansion (quadruplex), reciprocating piston-cylinder steam engine. This system achieved an actual thermal efficiency of 22.8%, which was remarkably high for its day. After about 1910, the production of large reciprocating piston-cylinder steam engines decreased rapidly. They were being replaced by a new prime mover technology, the steam turbine. Consequently, regeneration was temporarily discontinued until about 1920, at which point the steam turbine had been established as the preferred prime mover for large stationary power plants. After 1920, regeneration became standard practice in the design of large, vapor cycle, turbine, prime mover power plants. WHAT IS THE WORLD’S SMALLEST STEAM ENGINE? The world’s smallest steam engine was built using nanotechnology (the ability to create objects at the atomic scale). It is about 5 microns wide (approximately the size of a red blood cell), and was developed by Dr. Jeff Sniegowski at Sandia National Laboratories in Albuquerque, New Mexico. Steam is produced by a small electrical current that boils the water in a tiny boiler. The engine was built using computer chip technology by photographing and reducing an image to a very small size, then etching it on a silicon wafer. The etchings are done in layers to build up the three-dimensional working engine. However, you need an electron microscope to see it. 13.8 THE DEVELOPMENT OF THE STEAM TURBINE By the end of the 19th century, the large, slow-speed reciprocating piston-cylinder steam engine had reached its upper limit in size and complexity. When the maximum practical piston speed had been reached in reciprocating steam engine design, the only way to increase the work output further was to increase the physical size of the engine. The largest reciprocating steam engine ever built in the United States was constructed in 1891 by the E. P. Allis Company (renamed the Allis Chalmers Company in 1901) of Milwaukee, Wisconsin. It was installed as a pumping engine at the Chapin mine in Iron Mountain, Michigan, in 1892. It was a duplex steeple compound condensing engine with high-pressure cylinders 50. inches in diameter and low-pressure cylinders 100. inches in diameter, both with strokes of 10 ft. It was 54 ft high, 75 ft long, weighed 725 tons, and had a flywheel 40. ft in diameter. At its maximum speed of 10. rpm it could produce over 1200 hp. Meanwhile, a new heat engine prime mover technology was quickly being developed: the steam turbine. The word turbine was coined in 1822 from the Latin root word turbo, for“that which spins.” When it was coined it was applied only to water wheels (as in hydraulic or water turbines). A turbine is a prime mover in which mechanical rotating shaft work is produced by a steady flow of fluid through the system. The output work is produced by changing the momentum of the working fluid as it passes through the system (the turbine). Reciprocating prime mover output work, on the other hand, is produced by changing the pressure of a fixed mass of working fluid within the system (the piston-cylinder apparatus). There are two basic types of turbine designs: impulse and reaction. Both the impulse and reaction turbine concepts date from antiquity. The paddle-type water wheels developed in Italy in about 70 BC (and used throughout the world, well into the 20th century AD) were of the impulse type (Figure 13.24, left). Also, in the first century AD, a Greek known today only as Heron (or, in Latin, Hero) of Alexandria (Egypt) devised a simple reaction steam turbine (called an aeolipile) in which a hollow copper sphere was made to rotate by steam jetting out of four nozzles mounted perpendicular to the axis of rotation (see Figure 13.24, right). No practical use was then made of this device. However, it was known to James Watt and his contemporaries because they experimented with steam-driven reaction turbines of the Heron type and still found them impractical due to the extremely high rotational speeds required to make them efficient enough to be competitive with existing reciprocating steam engine technology. In the impulse turbine, high-velocity fluid jets from stationary nozzles impinge on a set of blades on a rotor. The impulse force generated by the momentum change of the fluid passing through these blades causes the
Page 2 and 3:
Modern Engineering Thermodynamics
Page 4 and 5:
Modern Engineering Thermodynamics R
Page 6 and 7:
Dedication WHAT IS AN ENGINEER AND
Page 8 and 9:
Contents PREFACE . . . . . . . . .
Page 10 and 11:
Contents ix 7.6 Heat Engines Runnin
Page 12 and 13:
Contents xi 14.13 Air Standard Gas
Page 14 and 15:
Preface TEXT OBJECTIVES This textbo
Page 16 and 17:
Preface xv Step 5. Write down the b
Page 18 and 19:
Acknowledgments I wish to acknowled
Page 20 and 21:
Resources That Accompany This Book
Page 22 and 23:
List of Symbols A a B COP CR c c p
Page 24 and 25:
Prologue PARIS FRANCE, 10:35 AM, AU
Page 26 and 27:
CHAPTER 1 The Beginning CONTENTS 1.
Page 28 and 29:
1.2 Why Is Thermodynamics Important
Page 30 and 31:
1.3 Getting Answers: A Basic Proble
Page 32 and 33:
1.5 How Do We Measure Things? 7 bei
Page 34 and 35:
1.6 Temperature Units 9 THE DEVELOP
Page 36 and 37:
1.7 Classical Mechanical and Electr
Page 38 and 39:
1.7 Classical Mechanical and Electr
Page 40 and 41:
1.9 Modern Units Systems 15 where M
Page 42 and 43:
1.10 Significant Figures 17 CRITICA
Page 44 and 45:
1.10 Significant Figures 19 WHAT AB
Page 46 and 47:
1.11 Potential and Kinetic Energies
Page 48 and 49:
1.11 Potential and Kinetic Energies
Page 50 and 51:
Summary 25 FIGURE 1.19 Case study 1
Page 52 and 53:
Problems 27 Problems (* indicates p
Page 54 and 55:
Problems 29 14. Determine the mass
Page 56 and 57:
Problems 31 49. Using the CGS units
Page 58 and 59:
CHAPTER 2 Thermodynamic Concepts CO
Page 60 and 61:
2.3 Phases of Matter 35 System boun
Page 62 and 63:
2.4 System States and Thermodynamic
Page 64 and 65:
2.6 Thermodynamic Processes 39 WHAT
Page 66 and 67:
2.7 Pressure and Temperature Scales
Page 68 and 69:
2.9 The Continuum Hypothesis 43 Sur
Page 70 and 71:
2.10 The Balance Concept 45 Solutio
Page 72 and 73:
2.11 The Conservation Concept 47 or
Page 74 and 75:
2.11 The Conservation Concept 49 Th
Page 76 and 77:
Summary 51 change in the mass of X
Page 78 and 79:
Problems 53 Problems (* indicates p
Page 80 and 81:
Problems 55 and Death rate = α 2 +
Page 82 and 83:
CHAPTER 3 Thermodynamic Properties
Page 84 and 85:
3.3 Fun with Mathematics 59 CRITICA
Page 86 and 87:
3.4 Some Exciting New Thermodynamic
Page 88 and 89:
3.6 Enthalpy 63 WHO WAS AMALIE EMMY
Page 90 and 91:
3.7 Phase Diagrams 65 WHO WAS EMMY
Page 92 and 93:
Pressure Vapor 3.7 Phase Diagrams 6
Page 94 and 95:
3.7 Phase Diagrams 69 WHAT IS A “
Page 96 and 97:
3.7 Phase Diagrams 71 considerable
Page 98 and 99:
3.8 Quality 73 10 5 300 C Critical
Page 100 and 101:
3.8 Quality 75 Although Eq. (3.26)
Page 102 and 103:
3.9 Thermodynamic Equations of Stat
Page 104 and 105:
Page 106 and 107:
Page 108 and 109:
Page 110 and 111:
3.10 Thermodynamic Tables 85 Critic
Page 112 and 113:
3.12 Thermodynamic Charts 87 vð100
Page 114 and 115:
3.13 Thermodynamic Property Softwar
Page 116 and 117:
Summary 91 and e = E/m = u + V2 2g
Page 118 and 119:
Problems 93 c. For a saturated mixt
Page 120 and 121:
Problems 95 specific enthalpy of sa
Page 122 and 123:
Problems 97 Table 3.23 Problem 65 M
Page 124 and 125:
CHAPTER 4 The First Law of Thermody
Page 126 and 127:
4.3 The First Law of Thermodynamics
Page 128 and 129:
4.3 The First Law of Thermodynamics
Page 130 and 131:
4.4 Energy Transport Mechanisms 105
Page 132 and 133:
4.5 Point and Path Functions 107 4.
Page 134 and 135:
4.6 Mechanical Work Modes of Energy
Page 136 and 137:
Page 138 and 139:
Page 140 and 141:
Page 142 and 143:
4.7 Nonmechanical Work Modes of Ene
Page 144 and 145:
Page 146 and 147:
Page 148 and 149:
Page 150 and 151:
4.9 Work Efficiency 125 In the case
Page 152 and 153:
4.12 Heat Modes of Energy Transport
Page 154 and 155:
4.13 Heat Transfer Modes 129 Table
Page 156 and 157:
4.14 A Thermodynamic Problem Solvin
Page 158 and 159:
4.14 A Thermodynamic Problem Solvin
Page 160 and 161:
4.15 How to Write a Thermodynamics
Page 162 and 163:
4.15 How to Write a Thermodynamics
Page 164 and 165:
Summary 139 The general open system
Page 166 and 167:
Problems 141 11.* Determine the hea
Page 168 and 169:
Problems 143 where K = 0.810 lbf. D
Page 170 and 171:
Problems 145 Table 4.12 Problem 67
Page 172 and 173:
CHAPTER 5 First Law Closed System A
Page 174 and 175:
5.2 Sealed, Rigid Containers 149 In
Page 176 and 177:
5.4 Power Plants 151 Step 7. Calcul
Page 178 and 179:
5.5 Incompressible Liquids 153 The
Page 180 and 181:
1Q 2 − 1 W 2 = mðu 2 − u 1 Þ
Page 182 and 183:
5.8 Closed System Unsteady State Pr
Page 184 and 185:
5.9 The Explosive Energy of Pressur
Page 186 and 187:
Problems 161 Problems (* indicates
Page 188 and 189:
Problems 163 31. A thermoelectric g
Page 190 and 191:
Problems 165 where v, T, and r are
Page 192 and 193:
CHAPTER 6 First Law Open System App
Page 194 and 195:
6.2 Mass Flow Energy Transport 169
Page 196 and 197:
6.3 Conservation of Energy and Cons
Page 198 and 199:
6.4 Flow Stream Specific Kinetic an
Page 200 and 201:
6.5 Nozzles and Diffusers 175 m (a)
Page 202 and 203:
6.5 Nozzles and Diffusers 177 We ar
Page 204 and 205:
6.6 Throttling Devices 179 These as
Page 206 and 207:
6.6 Throttling Devices 181 For an i
Page 208 and 209:
6.7 Throttling Calorimeter 183 The
Page 210 and 211:
6.8 Heat Exchangers 185 Convective
Page 212 and 213:
6.9 Shaft Work Machines 187 6.9 SHA
Page 214 and 215:
6.9 Shaft Work Machines 189 1 Basem
Page 216 and 217:
6.10 Open System Unsteady State Pro
Page 218 and 219:
Page 220 and 221:
Page 222 and 223:
Problems 197 we have _m R / _m D =
Page 224 and 225:
Page 226 and 227:
Problems 201 32.* A commercial slid
Page 228 and 229:
Summary 203 59. Incompressible liqu
Page 230 and 231:
CHAPTER 7 Second Law of Thermodynam
Page 232 and 233:
7.3 The Second Law of Thermodynamic
Page 234 and 235:
7.4 Carnot’s Heat Engine and the
Page 236 and 237:
7.4 Carnot’s Heat Engine and the
Page 238 and 239:
7.5 The Absolute Temperature Scale
Page 240 and 241:
7.5 The Absolute Temperature Scale
Page 242 and 243:
7.6 Heat Engines Running Backward 2
Page 244 and 245:
7.7 Clausius’s Definition of Entr
Page 246 and 247:
7.8 Numerical Values for Entropy 22
Page 248 and 249:
Page 250 and 251:
Page 252 and 253:
7.10 Differential Entropy Balance 2
Page 254 and 255:
7.11 Heat Transport of Entropy 229
Page 256 and 257:
7.13 Entropy Production Mechanisms
Page 258 and 259:
7.14 Heat Transfer Production of En
Page 260 and 261:
7.15 Work Mode Production of Entrop
Page 262 and 263:
7.15 Work Mode Production of Entrop
Page 264 and 265:
7.16 Phase Change Entropy Productio
Page 266 and 267:
Summary 241 ■ Indirect method inv
Page 268 and 269:
Problems 243 amount of work W irr i
Page 270 and 271:
Problems 245 a. If the heat pump is
Page 272 and 273:
Problems 247 51. Develop a program
Page 274 and 275:
CHAPTER 8 Second Law Closed System
Page 276 and 277:
8.2 Systems Undergoing Reversible P
Page 278 and 279:
Page 280 and 281:
Page 282 and 283:
8.3 Systems Undergoing Irreversible
Page 284 and 285:
Page 286 and 287:
Page 288 and 289:
Page 290 and 291:
Page 292 and 293:
Page 294 and 295:
Page 296 and 297:
8.4 Diffusional Mixing 271 Exercise
Page 298 and 299:
Summary 273 Note that this example
Page 300 and 301:
Problems 275 15. A 20.0 ft 3 tank c
Page 302 and 303:
Problems 277 46. a. Determine a for
Page 304 and 305:
CHAPTER 9 Second Law Open System Ap
Page 306 and 307:
9.4 Open System Entropy Balance Equ
Page 308 and 309:
9.4 Open System Entropy Balance Equ
Page 310 and 311:
9.5 Nozzles, Diffusers, and Throttl
Page 312 and 313:
9.5 Nozzles, Diffusers, and Throttl
Page 314 and 315:
9.6 Heat Exchangers 289 Exercises 1
Page 316 and 317:
9.6 Heat Exchangers 291 (T H ) (T H
Page 318 and 319:
9.7 Mixing 293 Now, _m air is given
Page 320 and 321:
9.7 Mixing 295 Critical value of y,
Page 322 and 323:
9.9 Unsteady State Processes in Ope
Page 324 and 325:
Page 326 and 327:
Page 328 and 329:
Page 330 and 331:
Page 332 and 333:
Page 334 and 335:
Problems 309 Multiplying this equat
Page 336 and 337:
Problems 311 entropy production rat
Page 338 and 339:
Problems 313 heat is added to the b
Page 340 and 341:
Problems 315 55.* Determine the max
Page 342 and 343:
Problems 317 The cavitation process
Page 344 and 345:
CHAPTER 10 Availability Analysis CO
Page 346 and 347:
10.3 What Are Conservative Forces?
Page 348 and 349:
10.6 Availability 323 WHAT IS A SYS
Page 350 and 351:
10.6 Availability 325 and the total
Page 352 and 353:
10.7 Closed System Availability Bal
Page 354 and 355:
10.7 Closed System Availability Bal
Page 356 and 357:
10.8 Flow Availability 331 EXAMPLE
Page 358 and 359:
s − s 0 = c ln T T 0 10.8 Flow Av
Page 360 and 361:
10.10 Modified Availability Rate Ba
Page 362 and 363:
10.10 Modified Availability Rate Ba
Page 364 and 365:
10.11 Energy Efficiency Based on th
Page 366 and 367:
Page 368 and 369:
Page 370 and 371:
Page 372 and 373:
Page 374 and 375:
Page 376 and 377:
Summary 351 In this problem, we hav
Page 378 and 379:
Summary 353 7. The general open sys
Page 380 and 381:
Problems 355 12.5 Btu/hr·ft ·R. I
Page 382 and 383:
Problems 357 flow rate of 15.0 lbm/
Page 384 and 385:
Problems 359 85. Create a specific
Page 386 and 387:
CHAPTER 11 More Thermodynamic Relat
Page 388 and 389:
11.2 Two New Properties: Helmholtz
Page 390 and 391:
11.2 Two New Properties: Helmholtz
Page 392 and 393:
11.4 Maxwell Equations 367 11.4 MAX
Page 394 and 395:
11.4 Maxwell Equations 369 then,
Page 396 and 397:
11.5 The Clapeyron Equation 371 and
Page 398 and 399:
11.6 Determining u, h, and s from p
Page 400 and 401:
Page 402 and 403:
Page 404 and 405:
11.7 Constructing Tables and Charts
Page 406 and 407:
11.8 Thermodynamic Charts 381 so th
Page 408 and 409:
11.9 Gas Tables 383 where p r is th
Page 410 and 411:
11.10 Compressibility Factor and Ge
Page 412 and 413:
Page 414 and 415:
Page 416 and 417:
Page 418 and 419:
Page 420 and 421:
Page 422 and 423:
11.11 Is Steam Ever an Ideal Gas? 3
Page 424 and 425:
Summary 399 equation, and a series
Page 426 and 427:
Problems 401 20.* Estimate h fg for
Page 428 and 429:
Problems 403 Design Problems The fo
Page 430 and 431:
CHAPTER 12 Mixtures of Gases and Va
Page 432 and 433:
12.2 Thermodynamic Properties of Ga
Page 434 and 435:
Page 436 and 437:
Page 438 and 439:
12.3 Mixtures of Ideal Gases 413 Th
Page 440 and 441:
12.3 Mixtures of Ideal Gases 415 Co
Page 442 and 443:
12.4 Psychrometrics 417 Finally, th
Page 444 and 445:
12.4 Psychrometrics 419 EXAMPLE 12.
Page 446 and 447:
12.6 The Sling Psychrometer 421 The
Page 448 and 449: 12.6 The Sling Psychrometer 423 p w
Page 450 and 451: 12.7 Air Conditioning 425 WHAT ENVI
Page 452 and 453: 12.8 Psychrometric Enthalpies 427 E
Page 454 and 455: 12.8 Psychrometric Enthalpies 429 o
Page 456 and 457: 12.9 Mixtures of Real Gases 431 Whe
Page 458 and 459: 12.9 Mixtures of Real Gases 433 and
Page 460 and 461: 12.9 Mixtures of Real Gases 435 The
Page 462 and 463: 12.9 Mixtures of Real Gases 437 Sol
Page 464 and 465: Summary 439 Last, we combine Dalton
Page 466 and 467: Problems 441 Problems (* indicates
Page 468 and 469: Problems 443 exhaust gas is an idea
Page 470 and 471: Problems 445 57.* Cooling towers ar
Page 472 and 473: CHAPTER 13 Vapor and Gas Power Cycl
Page 474 and 475: 13.2 Part I. Engines and Vapor Powe
Page 482 and 483: 13.4 Rankine Cycle 457 A B Reversib
Page 484 and 485: 13.5 Operating Efficiencies 459 For
Page 486 and 487: 13.5 Operating Efficiencies 461 13.
Page 488 and 489: 13.5 Operating Efficiencies 463 b.
Page 490 and 491: 13.5 Operating Efficiencies 465 Sta
Page 492 and 493: 13.6 Rankine Cycle with Superheat 4
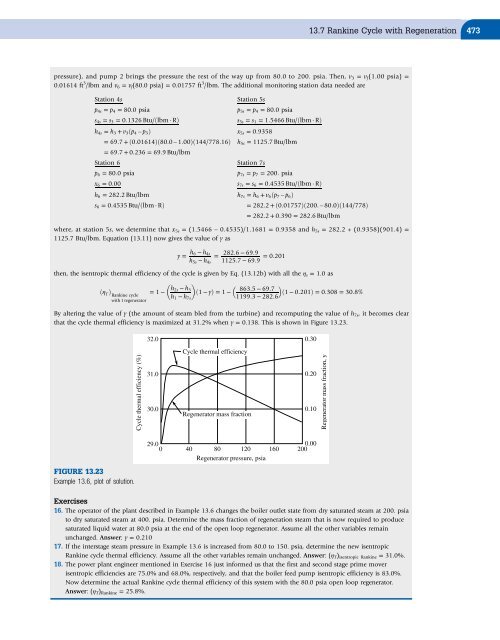
Page 494 and 495: 13.7 Rankine Cycle with Regeneratio
Page 496 and 497: 13.7 Rankine Cycle with Regeneratio
Page 500 and 501: 13.8 The Development of the Steam T
Page 502 and 503: 13.9 Rankine Cycle with Reheat 477
Page 504 and 505: 13.9 Rankine Cycle with Reheat 479
Page 506 and 507: 13.10 Modern Steam Power Plants 481
Page 512 and 513: 13.12 Air Standard Power Cycles 487
Page 514 and 515: 13.13 Stirling Cycle 489 Q H 4 1 4
Page 516 and 517: 13.14 Ericsson Cycle 491 Q H 4 1 3
Page 518 and 519: 13.15 Lenoir Cycle 493 Exercises 28
Page 520 and 521: 13.16 Brayton Cycle 495 Solution Us
Page 522 and 523: 13.16 Brayton Cycle 497 Equation (7
Page 524 and 525: 13.17 Aircraft Gas Turbine Engines
Page 526 and 527: 13.17 Aircraft Gas Turbine Engines
Page 528 and 529: 13.18 Otto Cycle 503 T Q H 1 1 1 v
Page 530 and 531: 13.18 Otto Cycle 505 Exercises 40.
Page 532 and 533: 13.18 Otto Cycle 507 and, since the
Page 534 and 535: 13.20 Miller Cycle 509 13.19.1 Mode
Page 536 and 537: 13.20 Miller Cycle 511 Then, from F
Page 538 and 539: 13.21 Diesel Cycle 513 to stroll on
Page 540 and 541: 13.21 Diesel Cycle 515 Solution a.
Page 542 and 543: 13.22 Modern Prime Mover Developmen
Page 544 and 545: 13.23 Second Law Analysis of Vapor
Page 546 and 547: 13.23 Second Law Analysis of Vapor
Page 548 and 549:
13.23 Second Law Analysis of Vapor
Page 550 and 551:
Summary 525 Fill port 160 mm End of
Page 552 and 553:
Problems 527 7. The thermal efficie
Page 554 and 555:
efficiency increase if the condense
Page 556 and 557:
Problems 531 horsepower hour. Assum
Page 558 and 559:
Problems 533 72. Determine the valu
Page 560 and 561:
CHAPTER 14 Vapor and Gas Refrigerat
Page 562 and 563:
14.3 Carnot Refrigeration Cycle 537
Page 564 and 565:
14.4 In the Beginning There Was Ice
Page 566 and 567:
14.4 In the Beginning There Was Ice
Page 568 and 569:
14.5 Vapor-Compression Refrigeratio
Page 570 and 571:
14.5 Vapor-Compression Refrigeratio
Page 572 and 573:
14.6 Refrigerants 547 T 3 2s 2 p 3
Page 574 and 575:
14.7 Refrigerant Numbers 549 14.7 R
Page 576 and 577:
14.7 Refrigerant Numbers 551 R-110
Page 578 and 579:
14.8 CFCs and the Ozone Layer 553 H
Page 580 and 581:
14.9 Cascade and Multistage Vapor-C
Page 582 and 583:
Page 584 and 585:
Page 586 and 587:
14.10 Absorption Refrigeration 561
Page 588 and 589:
14.11 Commercial and Household Refr
Page 590 and 591:
Page 592 and 593:
Page 594 and 595:
14.14 Reversed Brayton Cycle Refrig
Page 596 and 597:
14.14 Reversed Brayton Cycle Refrig
Page 598 and 599:
14.15 Reversed Stirling Cycle Refri
Page 600 and 601:
14.16 Miscellaneous Refrigeration T
Page 602 and 603:
14.16 Miscellaneous Refrigeration T
Page 604 and 605:
14.18 Second Law Analysis of Refrig
Page 606 and 607:
14.18 Second Law Analysis of Refrig
Page 608 and 609:
2. The coefficient of performance o
Page 610 and 611:
Problems 585 13.* A refrigeration u
Page 612 and 613:
Problems 587 Loop B Station 1B Stat
Page 614 and 615:
Problems 589 under these conditions
Page 616 and 617:
CHAPTER 15 Chemical Thermodynamics
Page 618 and 619:
15.2 Stoichiometric Equations 593 1
Page 620 and 621:
15.2 Stoichiometric Equations 595 C
Page 622 and 623:
15.3 Organic Fuels 597 ANSWERS SOME
Page 624 and 625:
15.4 Fuel Modeling 599 Hydrocarbon
Page 626 and 627:
15.4 Fuel Modeling 601 equation, si
Page 628 and 629:
15.5 Standard Reference State 603 I
Page 630 and 631:
15.6 Heat of Formation 605 and H 2
Page 632 and 633:
15.7 Heat of Reaction 607 EXAMPLE 1
Page 634 and 635:
15.7 Heat of Reaction 609 CRITICAL
Page 636 and 637:
15.7 Heat of Reaction 611 Then, h P
Page 638 and 639:
15.8 Adiabatic Flame Temperature 61
Page 640 and 641:
Page 642 and 643:
Page 644 and 645:
15.9 Maximum Explosion Pressure 619
Page 646 and 647:
15.10 Entropy Production in Chemica
Page 648 and 649:
15.10 Entropy Production in Chemica
Page 650 and 651:
15.11 Entropy of Formation and Gibb
Page 652 and 653:
15.12 Chemical Equilibrium and Diss
Page 654 and 655:
Page 656 and 657:
Page 658 and 659:
H 2 O !ð1 − yÞH 2 O + yðv H2
Page 660 and 661:
15.14 The van’t Hoff Equation 635
Page 662 and 663:
15.15 Fuel Cells 637 Anode Electrol
Page 664 and 665:
15.15 Fuel Cells 639 The maximum po
Page 666 and 667:
15.16 Chemical Availability 641 and
Page 668 and 669:
ðn i /n fuel Þðc pi Þ E system
Page 670 and 671:
Problems 645 where j = 4n + m kgmol
Page 672 and 673:
Problems 647 c. The percent excess
Page 674 and 675:
Problems 649 77. Determine the mola
Page 676 and 677:
CHAPTER 16 Compressible Fluid Flow
Page 678 and 679:
16.3 Isentropic Stagnation Properti
Page 680 and 681:
16.4 The Mach Number 655 Note that
Page 682 and 683:
16.4 The Mach Number 657 Table 16.1
Page 684 and 685:
16.4 The Mach Number 659 Since for
Page 686 and 687:
16.5 Converging-Diverging Flows 661
Page 688 and 689:
16.5 Converging-Diverging Flows 663
Page 690 and 691:
16.6 Choked Flow 665 T a a p a = co
Page 692 and 693:
16.6 Choked Flow 667 Exercises 16.
Page 694 and 695:
16.7 Reynolds Transport Theorem 669
Page 696 and 697:
16.7 Reynolds Transport Theorem 671
Page 698 and 699:
16.8 Linear Momentum Rate Balance 6
Page 700 and 701:
16.9 Shock Waves 675 16.9 SHOCK WAV
Page 702 and 703:
16.9 Shock Waves 677 and, for an id
Page 704 and 705:
16.9 Shock Waves 679 6 5 4 S P /(m
Page 706 and 707:
16.10 Nozzle and Diffuser Efficienc
Page 708 and 709:
16.10 Nozzle and Diffuser Efficienc
Page 710 and 711:
Summary 685 Since for a diffuser, M
Page 712 and 713:
Page 714 and 715:
43. 0.800 lbm/s of air passes throu
Page 716 and 717:
Problems 691 A plot of this functio
Page 718 and 719:
CHAPTER 17 Thermodynamics of Biolog
Page 720 and 721:
17.3 Thermodynamics of Biological C
Page 722 and 723:
17.3 Thermodynamics of Biological C
Page 724 and 725:
17.4 Energy Conversion Efficiency o
Page 726 and 727:
17.4 Energy Conversion Efficiency o
Page 728 and 729:
17.5 Metabolism 703 Table 17.3 Brea
Page 730 and 731:
17.6 Thermodynamics of Nutrition an
Page 732 and 733:
Page 734 and 735:
Page 736 and 737:
17.7 Limits to Biological Growth 71
Page 738 and 739:
17.7 Limits to Biological Growth 71
Page 740 and 741:
17.8 Locomotion Transport Number 71
Page 742 and 743:
17.9 Thermodynamics of Aging and De
Page 744 and 745:
17.9 Thermodynamics of Aging and De
Page 746 and 747:
1/3 V most efficient = P o ρAC D S
Page 748 and 749:
Problems 723 a. If the monster cons
Page 750 and 751:
Problems 725 the officer asks Paul
Page 752 and 753:
CHAPTER 18 Introduction to Statisti
Page 754 and 755:
18.3 Kinetic Theory of Gases 729 3.
Page 756 and 757:
U trans = 3 2 NkT (Continued ) 18.3
Page 758 and 759:
18.4 Intermolecular Collisions 733
Page 760 and 761:
18.5 Molecular Velocity Distributio
Page 762 and 763:
18.5 Molecular Velocity Distributio
Page 764 and 765:
18.6 Equipartition of Energy 739 We
Page 766 and 767:
18.7 Introduction to Mathematical P
Page 768 and 769:
Page 770 and 771:
Page 772 and 773:
18.8 Quantum Statistical Thermodyna
Page 774 and 775:
18.9 Three Classical Quantum Statis
Page 776 and 777:
18.11 Monatomic Maxwell-Boltzmann G
Page 778 and 779:
18.12 Diatomic Maxwell-Boltzmann Ga
Page 780 and 781:
18.12 Diatomic Maxwell-Boltzmann Ga
Page 782 and 783:
18.13 Polyatomic Maxwell-Boltzmann
Page 784 and 785:
Summary 759 In this chapter, we sum
Page 786 and 787:
Problems 761 4. Find the temperatur
Page 788 and 789:
CHAPTER 19 Introduction to Coupled
Page 790 and 791:
19.3 Linear Phenomenological Equati
Page 792 and 793:
19.4 Thermoelectric Coupling 767 Eq
Page 794 and 795:
19.4 Thermoelectric Coupling 769 Th
Page 796 and 797:
19.4 Thermoelectric Coupling 771 wh
Page 798 and 799:
19.4 Thermoelectric Coupling 773 Th
Page 800 and 801:
19.4 Thermoelectric Coupling 775 b.
Page 802 and 803:
19.5 Thermomechanical Coupling 777
Page 804 and 805:
Page 806 and 807:
Page 808 and 809:
water), it seems reasonable that li
Page 810 and 811:
Problems 785 b. For a Knudson gas,
Page 812 and 813:
Appendix A: Physical Constants and
Page 814 and 815:
Appendix B: Greek and Latin Origins
Page 816 and 817:
Appendix B 791 Table B.4 Plural End
Page 818 and 819:
Index Page numbers followed by f in
Page 820 and 821:
Index 795 E e (specific energy), 10
Page 822 and 823:
Index 797 Isobaric coefficient of v
Page 824 and 825:
Index 799 Ranque, Georges Joseph, 3
Page 826 and 827:
Index 801 William III, King of Engl
show all

Modern Engineering Thermodynamics

Create successful ePaper yourself

Delete template?

Save as template?