- Seite 1 und 2:
Herbert Möller Elementare Zahlenth
- Seite 3 und 4:
Vorwort Dieses Buch ist aus mehrere
- Seite 5 und 6:
Inhaltsverzeichnis Vorwort 3 Inhalt
- Seite 7 und 8:
Kapitel 1 Die natürlichen Zahlen 1
- Seite 9 und 10:
1.1 Grundlegung 9 Wie üblich werde
- Seite 11 und 12:
1.2 Die Beweissätze 11 Definition
- Seite 13 und 14:
1.3 Verknüpfungen von natürlichen
- Seite 15 und 16:
1.4 Einführung in die elementare Z
- Seite 17 und 18:
Kapitel 2 Teilbarkeit 2.1 Teiler vo
- Seite 19 und 20:
2.2 Größter gemeinsamer Teiler 19
- Seite 21 und 22:
2.2 Größter gemeinsamer Teiler 21
- Seite 23 und 24: 2.3 Lineare diophantische Gleichung
- Seite 25 und 26: 2.3 Lineare diophantische Gleichung
- Seite 27 und 28: 2.3 Lineare diophantische Gleichung
- Seite 29 und 30: 2.3 Lineare diophantische Gleichung
- Seite 31 und 32: 2.4 Gaußsche Erkundungsstrategie 3
- Seite 33 und 34: 2.4 Gaußsche Erkundungsstrategie 3
- Seite 35 und 36: 2.5 Pythagoreische Tripel 35 Gehen
- Seite 37 und 38: 2.5 Pythagoreische Tripel 37 Ration
- Seite 39 und 40: 2.5 Pythagoreische Tripel 39 Beweis
- Seite 41 und 42: 2.6 g-adische Zahlendarstellung 41
- Seite 43 und 44: 2.7 Aufgaben und Probleme 43 2.7 Au
- Seite 45 und 46: 2.7 Aufgaben und Probleme 45 Proble
- Seite 47 und 48: Kapitel 3 Elementare Primzahltheori
- Seite 49 und 50: 3.2 Der Hauptsatz der elementaren Z
- Seite 51 und 52: 3.2 Der Hauptsatz der elementaren Z
- Seite 53 und 54: 3.3 Anwendungen des Hauptsatzes 53
- Seite 55 und 56: 3.3 Anwendungen des Hauptsatzes 55
- Seite 57 und 58: 3.4 Vollkommene Zahlen und speziell
- Seite 59 und 60: 3.4 Vollkommene Zahlen und speziell
- Seite 61 und 62: 3.4 Vollkommene Zahlen und speziell
- Seite 63 und 64: 3.5 Verteilung der Primzahlen 63 Un
- Seite 65 und 66: 3.5 Verteilung der Primzahlen 65 Di
- Seite 67 und 68: 3.5 Verteilung der Primzahlen 67 Di
- Seite 69 und 70: 3.5 Verteilung der Primzahlen 69 Du
- Seite 71 und 72: 3.6 Ausblick auf Resultate der anal
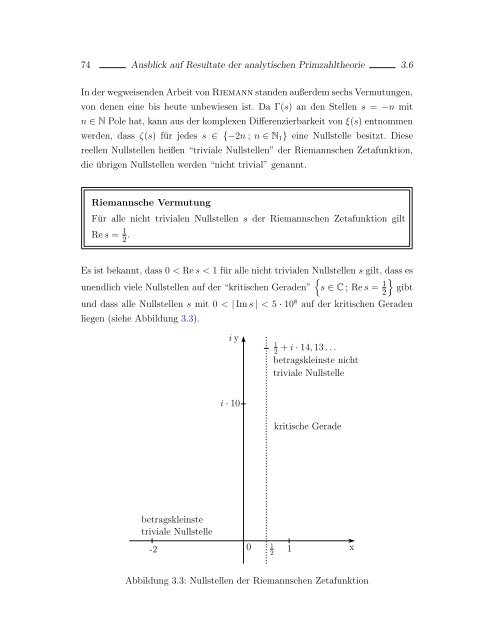
- Seite 73: 3.6 Ausblick auf Resultate der anal
- Seite 77 und 78: 3.7 Aufgaben und Probleme 77 [Hinwe
- Seite 79 und 80: 3.7 Aufgaben und Probleme 79 [Hinwe
- Seite 81 und 82: 3.7 Aufgaben und Probleme 81 Proble
- Seite 83 und 84: Kapitel 4 Kongruenzen 4.1 Die Kongr
- Seite 85 und 86: 4.2 Restklassen 85 Bezeichnung des
- Seite 87 und 88: 4.2 Restklassen 87 Beweis (drei Tei
- Seite 89 und 90: 4.2 Restklassen 89 wobei die letzte
- Seite 91 und 92: 4.3 Kongruenzsätze 91 4.3 Kongruen
- Seite 93 und 94: 4.4 Eigenschaften der Restsysteme 9
- Seite 95 und 96: 4.4 Eigenschaften der Restsysteme 9
- Seite 97 und 98: 4.4 Eigenschaften der Restsysteme 9
- Seite 99 und 100: 4.5 Die Eulersche ϕ-Funktion 99 Un
- Seite 101 und 102: 4.6 Kongruenzen mit einer Unbekannt
- Seite 103 und 104: 4.6 Kongruenzen mit einer Unbekannt
- Seite 105 und 106: 4.6 Kongruenzen mit einer Unbekannt
- Seite 107 und 108: 4.7 Potenzreste 107 Satz über Modu
- Seite 109 und 110: 4.7 Potenzreste 109 Beweis (direkt,
- Seite 111 und 112: 4.7 Potenzreste 111 Beweis (direkt,
- Seite 113 und 114: 4.7 Potenzreste 113 Beweis (direkt,
- Seite 115 und 116: 4.7 Potenzreste 115 formulierung di
- Seite 117 und 118: 4.7 Potenzreste 117 jektiv ist. Der
- Seite 119 und 120: 4.7 Potenzreste 119 Beweis (direkt
- Seite 121 und 122: 4.8 Ordnungen, Primitivwurzeln und
- Seite 123 und 124: 4.8 Ordnungen, Primitivwurzeln und
- Seite 125 und 126:
4.8 Ordnungen, Primitivwurzeln und
- Seite 127 und 128:
4.8 Ordnungen, Primitivwurzeln und
- Seite 129 und 130:
4.8 Ordnungen, Primitivwurzeln und
- Seite 131 und 132:
4.9 Aufgaben und Probleme 131 Aufga
- Seite 133 und 134:
4.9 Aufgaben und Probleme 133 Probl
- Seite 135 und 136:
4.9 Aufgaben und Probleme 135 Probl
- Seite 137 und 138:
Kapitel 5 Ergänzungen 5.1 Die Falt
- Seite 139 und 140:
5.1 Die Faltung zahlentheoretischer
- Seite 141 und 142:
5.2 Darstellung als Summe von Quadr
- Seite 143 und 144:
5.2 Darstellung als Summe von Quadr
- Seite 145 und 146:
5.2 Darstellung als Summe von Quadr
- Seite 147 und 148:
5.2 Darstellung als Summe von Quadr
- Seite 149 und 150:
5.2 Darstellung als Summe von Quadr
- Seite 151 und 152:
5.3 Binäre quadratische Formen und
- Seite 153 und 154:
5.3 Binäre quadratische Formen und
- Seite 155 und 156:
5.3 Binäre quadratische Formen und
- Seite 157 und 158:
5.3 Binäre quadratische Formen und
- Seite 159 und 160:
5.3 Binäre quadratische Formen und
- Seite 161 und 162:
5.3 Binäre quadratische Formen und
- Seite 163 und 164:
5.4 Quadratische Zahlkörper 163 5.
- Seite 165 und 166:
5.4 Quadratische Zahlkörper 165 Be
- Seite 167 und 168:
5.4 Quadratische Zahlkörper 167 m
- Seite 169 und 170:
5.4 Quadratische Zahlkörper 169 (
- Seite 171 und 172:
5.4 Quadratische Zahlkörper 171 so
- Seite 173 und 174:
5.4 Quadratische Zahlkörper 173 wa
- Seite 175 und 176:
5.4 Quadratische Zahlkörper 175 (1
- Seite 177 und 178:
5.4 Quadratische Zahlkörper 177 (5
- Seite 179 und 180:
5.4 Quadratische Zahlkörper 179 k
- Seite 181 und 182:
Kapitel 6 Problemlösestrategien in
- Seite 183 und 184:
6.2 Heuristikbücher 183 Schule des
- Seite 185 und 186:
6.2 Heuristikbücher 185 Vorbild un
- Seite 187 und 188:
6.2 Heuristikbücher 187 raten und
- Seite 189 und 190:
6.2 Heuristikbücher 189 Problemen
- Seite 191 und 192:
6.3 Problemlösestrategien 191 Die
- Seite 193 und 194:
6.3 Problemlösestrategien 193 Gau
- Seite 195 und 196:
6.3 Problemlösestrategien 195 in d
- Seite 197 und 198:
6.3 Problemlösestrategien 197 7x 2
- Seite 199 und 200:
6.3 Problemlösestrategien 199 Prob
- Seite 201 und 202:
6.3 Problemlösestrategien 201 ( m+
- Seite 203 und 204:
6.3 Problemlösestrategien 203 sind
- Seite 205 und 206:
6.3 Problemlösestrategien 205 Prob
- Seite 207 und 208:
6.3 Problemlösestrategien 207 Sind
- Seite 209 und 210:
6.3 Problemlösestrategien 209 Rüc
- Seite 211 und 212:
6.3 Problemlösestrategien 211 Dami
- Seite 213 und 214:
6.3 Problemlösestrategien 213 P 2
- Seite 215 und 216:
6.3 Problemlösestrategien 215 so e
- Seite 217 und 218:
6.3 Problemlösestrategien 217 (6.2
- Seite 219 und 220:
6.3 Problemlösestrategien 219 Prob
- Seite 221 und 222:
6.3 Problemlösestrategien 221 wobe
- Seite 223 und 224:
6.3 Problemlösestrategien 223 r(r
- Seite 225 und 226:
6.3 Problemlösestrategien 225 Man
- Seite 227 und 228:
6.3 Problemlösestrategien 227 gel
- Seite 229 und 230:
6.3 Problemlösestrategien 229 Vera
- Seite 231 und 232:
6.3 Problemlösestrategien 231 im r
- Seite 233 und 234:
6.4 Hinweise zu den gestellten Prob
- Seite 235 und 236:
Satzverzeichnis Kardinalzahlpostula
- Seite 237 und 238:
Satzverzeichnis 237 Satz über Modu
- Seite 239 und 240:
GNU Free Documentation License Vers
- Seite 241 und 242:
GNU Free Documentation License 241
- Seite 243 und 244:
GNU Free Documentation License 243
- Seite 245 und 246:
GNU Free Documentation License 245
- Seite 247 und 248:
Literaturverzeichnis [1] Borewicz,
- Seite 249 und 250:
Index Abel, N. H., 96 Bernoulli, Ja
- Seite 251 und 252:
Index 251 Exponentenvergleichsstrat
- Seite 253 und 254:
Index 253 periodische Folge, 126 Pe