Mélanges de GLMs et nombre de composantes : application ... - Scor

4.2. Sélection de modèle mélange
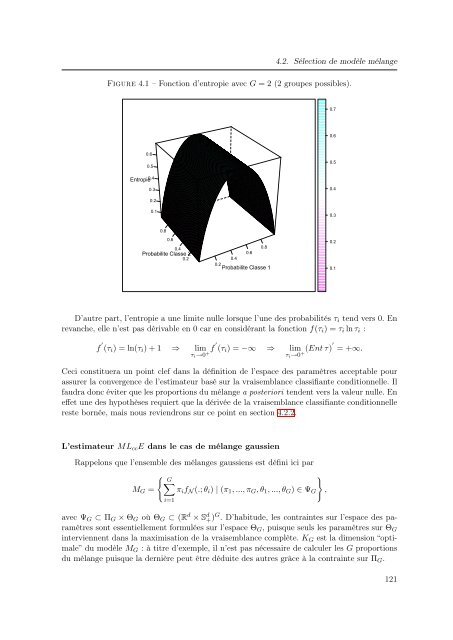
Figure 4.1 – Fonction d’entropie avec G = 2 (2 groupes possibles).
Fonction d'entropie
0.7
0.6
0.6
0.5
0.5
Entropie0.4
0.3
0.4
0.2
0.1
0.3
0.8
0.6
0.4
Probabilite Classe 2
0.2
0.8
0.6
0.4
0.2
Probabilite Classe 1
0.2
0.1
D’autre part, l’entropie a une limite nulle lorsque l’une des probabilités τ i tend vers 0. En
revanche, elle n’est pas dérivable en 0 car en considérant la fonction f(τ i ) = τ i ln τ i :
f ′ (τ i ) = ln(τ i ) + 1 ⇒ lim
τ i →0 +f ′ (τ i ) = −∞ ⇒ lim
τ i →0 +(Ent τ)′ = +∞.
Ceci constituera un point clef dans la définition de l’espace des paramètres acceptable pour
assurer la convergence de l’estimateur basé sur la vraisemblance classifiante conditionnelle. Il
faudra donc éviter que les proportions du mélange a posteriori tendent vers la valeur nulle. En
effet une des hypothèses requiert que la dérivée de la vraisemblance classifiante conditionnelle
reste bornée, mais nous reviendrons sur ce point en section 4.2.2.
L’estimateur ML cc E dans le cas de mélange gaussien
Rappelons que l’ensemble des mélanges gaussiens est défini ici par
{ G
}
∑
M G = π i f N (.; θ i ) | (π 1 , ..., π G , θ 1 , ..., θ G ) ∈ Ψ G ,
i=1
avec Ψ G ⊂ Π G × Θ G où Θ G ⊂ (R d × S d +) G . D’habitude, les contraintes sur l’espace des paramètres
sont essentiellement formulées sur l’espace Θ G , puisque seuls les paramètres sur Θ G
interviennent dans la maximisation de la vraisemblance complète. K G est la dimension “optimale”
du modèle M G : à titre d’exemple, il n’est pas nécessaire de calculer les G proportions
du mélange puisque la dernière peut être déduite des autres grâce à la contrainte sur Π G .
121