Mélanges de GLMs et nombre de composantes : application ... - Scor

B.1.3
Plus loin dans la théorie des CART
Spécification des règles binaires
B.1. Méthode CART
Criterion 1. Ces règles dépendent seulement d’un seuil µ et d’ une variable x l , 1 ≤ l ≤ d :
– x l ≤ µ, µ ∈ R dans le cas d’une variable continue ordonnée (si nous avons m valeurs
distinctes pour x l , l’ensemble des valeurs possibles card(D) vaut M - 1) ;
– x l ∈ µ où µ est un sous-ensemble de {µ 1 , µ 2 , ..., µ M } et les µ m sont les modalités de la
variable catégorielle (dans ce cas le cardinal du sous-ensemble D des règles binaires vaut
2 M−1 − 1).
Qu’est ce qu’une fonction d’impureté ?
Définition. Une fonction d’impureté est une fonction réelle g définie sur un ensemble de
probabilités discrètes d’un ensemble fini :
symétrique en p 1 , p 2 , ..., p J et qui vérifie :
g : (p 1 , p 2 , ..., p J ) → g(p 1 , p 2 , ..., p J ),
1. le maximum de g est à l’équiprobabilité : argmax g(p 1 , p 2 , ..., p J ) = ( 1
J , 1 J , ..., 1 J
)
,
2. le minimum de g est obtenu par les “dirac" : argmin g(p 1 , p 2 , ..., p J ) ∈ {e 1 , ..., e J }, où
e j est le j eme élément dans la base canonique deR J .
Différentes fonctions d’impureté
D’habitude nous considérons les fonctions suivantes (qui satisfont le critère de concavité) :
• impur(t) = - ∑ J
j=1 p(j|t) ln(p(j|t)) ; cp
size of tree
1 2 3 6 16 22 35 54 69 83 98 118 140 175
X-val Relative Error
0.2 0.4 0.6 0.8 1.0
Inf 0.043 0.00049 0.00032 0.00019 1e-04 5.3e-05 0
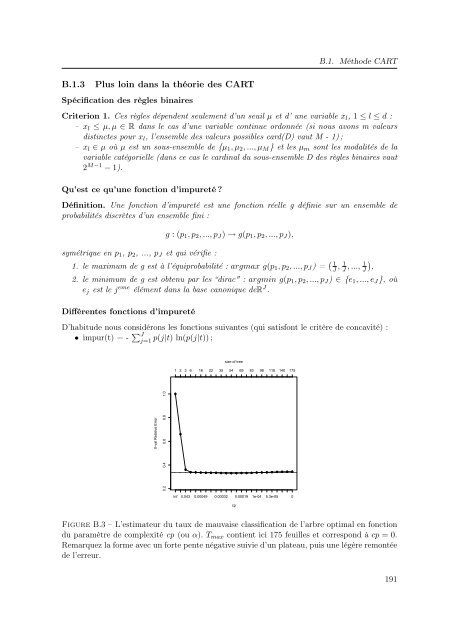
Figure B.3 – L’estimateur du taux de mauvaise classification de l’arbre optimal en fonction
du paramètre de complexité cp (ou α). T max contient ici 175 feuilles et correspond à cp = 0.
Remarquez la forme avec un forte pente négative suivie d’un plateau, puis une légère remontée
de l’erreur.
191