Identification d'efforts aux limites des poutres et plaques en flexion ...

CHAPITRE 5. RECONSTRUCTION DE L’EFFORT TRANCHANT ET DU MOMENT
FLÉCHISSANT : CAS D’UNE PLAQUE EN FLEXION
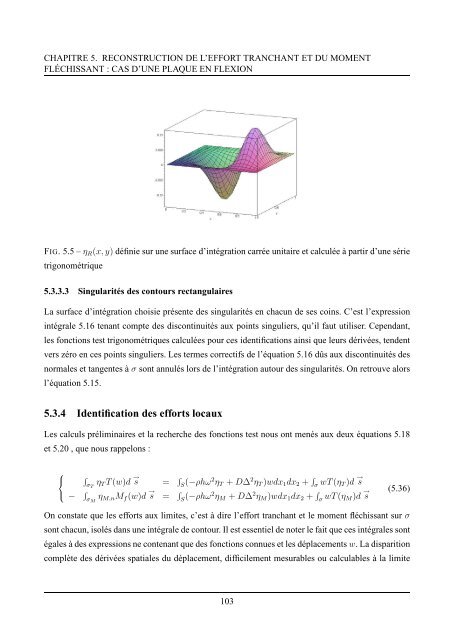
FIG. 5.5 – η R (x, y) définie sur une surface d’intégration carrée unitaire et calculée à partir d’une série
trigonométrique
5.3.3.3 Singularités des contours rectangulaires
La surface d’intégration choisie présente des singularités en chacun de ses coins. C’est l’expression
intégrale 5.16 tenant compte des discontinuités aux points singuliers, qu’il faut utiliser. Cependant,
les fonctions test trigonométriques calculées pour ces identifications ainsi que leurs dérivées, tendent
vers zéro en ces points singuliers. Les termes correctifs de l’équation 5.16 dûs aux discontinuités des
normales et tangentes à σ sont annulés lors de l’intégration autour des singularités. On retrouve alors
l’équation 5.15.
5.3.4 Identification des efforts locaux
Les calculs préliminaires et la recherche des fonctions test nous ont menés aux deux équations 5.18
et 5.20 , que nous rappelons :
⎧
⎨
⎩
−
∫
σ T
η T T(w)d → s = ∫ S (−ρhω2 η T + D∆ 2 η T )wdx 1 dx 2 + ∫ σ wT(η T)d → s
∫
σ M
η M,n M f (w)d → s = ∫ S (−ρhω2 η M + D∆ 2 η M )wdx 1 dx 2 + ∫ σ wT(η M)d → s
(5.36)
On constate que les efforts aux limites, c’est à dire l’effort tranchant et le moment fléchissant sur σ
sont chacun, isolés dans une intégrale de contour. Il est essentiel de noter le fait que ces intégrales sont
égales à des expressions ne contenant que des fonctions connues et les déplacements w. La disparition
complète des dérivées spatiales du déplacement, difficilement mesurables ou calculables à la limite
103