Identification d'efforts aux limites des poutres et plaques en flexion ...

CHAPITRE 2. APPROXIMATIONS ET INCERTITUDES : CAS D’UNE POUTRE EN FLEXION
5
4
3
Niveau d’erreur : ε T
(dB)
2
1
0
−1
−2
−3
−4
−5
0 1 2 3 4 5 6 7
Nombre d’onde dans l’intervalle d’intégration
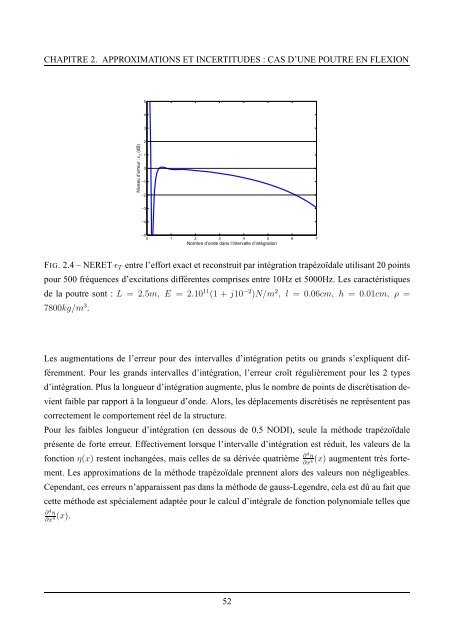
FIG. 2.4 – NERET ǫ T entre l’effort exact et reconstruit par intégration trapézoïdale utilisant 20 points
pour 500 fréquences d’excitations différentes comprises entre 10Hz et 5000Hz. Les caractéristiques
de la poutre sont : L = 2.5m, E = 2.10 11 (1 + j10 −2 )N/m 2 , l = 0.06cm, h = 0.01cm, ρ =
7800kg/m 3 .
Les augmentations de l’erreur pour des intervalles d’intégration petits ou grands s’expliquent différemment.
Pour les grands intervalles d’intégration, l’erreur croît régulièrement pour les 2 types
d’intégration. Plus la longueur d’intégration augmente, plus le nombre de points de discrétisation devient
faible par rapport à la longueur d’onde. Alors, les déplacements discrétisés ne représentent pas
correctement le comportement réel de la structure.
Pour les faibles longueur d’intégration (en dessous de 0.5 NODI), seule la méthode trapézoïdale
présente de forte erreur. Effectivement lorsque l’intervalle d’intégration est réduit, les valeurs de la
fonction η(x) restent inchangées, mais celles de sa dérivée quatrième ∂4 η
∂x 4 (x) augmentent très fortement.
Les approximations de la méthode trapézoïdale prennent alors des valeurs non négligeables.
Cependant, ces erreurs n’apparaissent pas dans la méthode de gauss-Legendre, cela est dû au fait que
cette méthode est spécialement adaptée pour le calcul d’intégrale de fonction polynomiale telles que
∂ 4 η
∂x 4 (x).
52