Identification d'efforts aux limites des poutres et plaques en flexion ...

CHAPITRE 6. APPROXIMATIONS ET INCERTITUDES : CAS D’UNE PLAQUE EN FLEXION
se projeter sur les axes x ou y donnant deux composants. Cependant, pour simplifier l’analyse on
utilisera uniquement le nombre d’onde naturel des plaques infinies, défini par :
√
ρh
k =
D√ 4 ω (6.17)
Par analogie avec le cas monodimensionnel, on cherche à caractériser l’erreur en fonction du paramètre
k × L, où L est la largeur de la surface d’intégration.
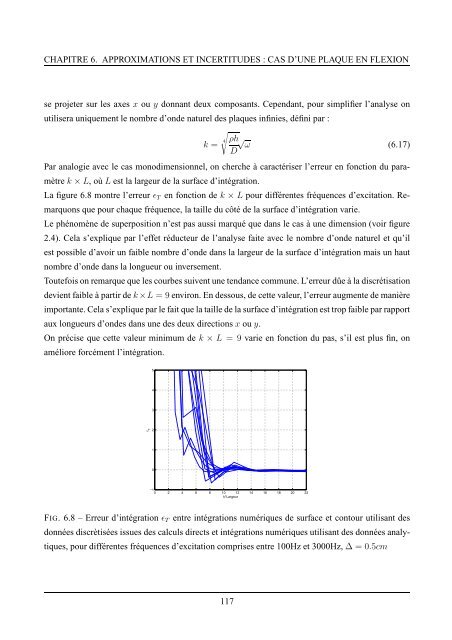
La figure 6.8 montre l’erreur ǫ T en fonction de k × L pour différentes fréquences d’excitation. Remarquons
que pour chaque fréquence, la taille du côté de la surface d’intégration varie.
Le phénomène de superposition n’est pas aussi marqué que dans le cas à une dimension (voir figure
2.4). Cela s’explique par l’effet réducteur de l’analyse faite avec le nombre d’onde naturel et qu’il
est possible d’avoir un faible nombre d’onde dans la largeur de la surface d’intégration mais un haut
nombre d’onde dans la longueur ou inversement.
Toutefois on remarque que les courbes suivent une tendance commune. L’erreur dûe à la discrétisation
devient faible à partir de k ×L = 9 environ. En dessous, de cette valeur, l’erreur augmente de manière
importante. Cela s’explique par le fait que la taille de la surface d’intégration est trop faible par rapport
aux longueurs d’ondes dans une des deux directions x ou y.
On précise que cette valeur minimum de k × L = 9 varie en fonction du pas, s’il est plus fin, on
améliore forcément l’intégration.
5
4
3
ε T
2
1
0
−1
0 2 4 6 8 10 12 14 16 18 20 22
k*Largeur
FIG. 6.8 – Erreur d’intégration ǫ T entre intégrations numériques de surface et contour utilisant des
données discrètisées issues des calculs directs et intégrations numériques utilisant des données analytiques,
pour différentes fréquences d’excitation comprises entre 100Hz et 3000Hz, ∆ = 0.5cm
117