Excel parancsfájlok felhasználása a statisztikai elemzésekben Írta ...

k
∑
r
fx i i
i= 1 mr
=
n
Ha a r=1, az ún. elsőrendű momentum a számtani átlag, m1= x.
Definiálható valamely tetszőlegesen megválasztott „a” értékre vonatkozó r-ed rendű momentum is, ha
a = x,
akkor ez az r-ed rendű centrális momentum súlyozott esetben:
r
fi( xi − x)
i= 1 mr( c)
=
n
Az első rendű centrális momentum, m1( c) 0
2
másod rendű centrális momentum megegyezik a szórásnégyzettel. m2( c ) = σ .
Empirikus eloszlástípusok. Az aszimmetria és a ferdeség mérésére szolgáló mutatók
k
∑
= , mivel az átlagtól mért eltérések algebrai összege 0. A
A gyakorisági eloszlások elemzése a gyakorisági görbe alakjának vizsgálatát jelenti. Az empirikus eloszlást
jellemző grafikus ábrát, a hisztogramot, illetve gyakorisági poligont, összehasonlítjuk a normális eloszlás
szimmetrikus gyakorisági görbéjével. A gyakorisági poligon felrajzolása során az osztályközepeknél
felmért gyakoriságok pontjait (ezek a hisztogramok oszlopközepének felelnek meg) összekötjük. Az
ún. egymóduszú eloszlás esetében, azt vizsgáljuk, hogy az empirikus eloszlásunk szimmetrikusnak tekinthető-e,
vagy a görbe, valamelyik széle felé jobban elnyúlik. Ez utóbbi esetben jobb, vagy bal oldali
aszimmetriáról beszélünk. A gyakorisági görbe alakjáról a grafikus ábra és a középértékek nagyságrendje
már tájékoztat. Szimmetrikus tekinthető empirikus eloszlások esetén a számtani átlag, a medián és a
módusz értéke közel azonos.
Jobb oldali aszimmetriánál az említett három középérték közül a módusz értéke a legkisebb, bal oldali
aszimmetriánál pedig a számtani átlagé. Jobb oldali aszimmetriájú eloszlás esetén, a görbe a csúcspontját
valamilyen alacsonyabb i x értéknél veszi fel, a magasabb x i értékek felé haladva a gyakoriságok egyre
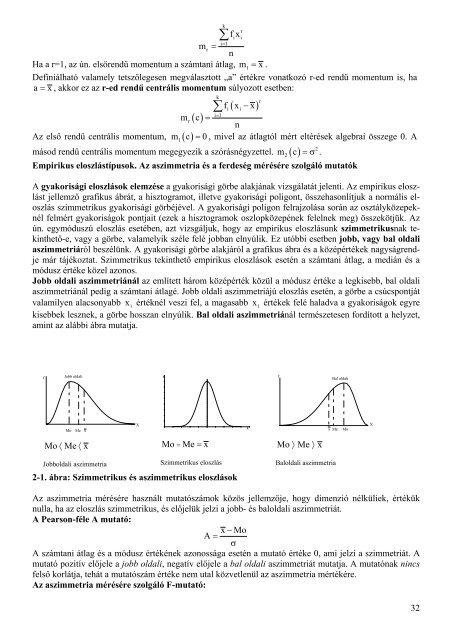
kisebbek lesznek, a görbe hosszan elnyúlik. Bal oldali aszimmetriánál természetesen fordított a helyzet,
amint az alábbi ábra mutatja.
f
Jobb oldali
Mo Me x
Mo 〈 Me 〈
x
Jobboldali aszimmetria
X
f
Mo = Me =
x
Szimmetrikus eloszlás
2-1. ábra: Szimmetrikus és aszimmetrikus eloszlások
X
f
Mo 〉 Me 〉
x
Baloldali aszimmetria
Bal oldali
xMe Mo
Az aszimmetria mérésére használt mutatószámok közös jellemzője, hogy dimenzió nélküliek, értékük
nulla, ha az eloszlás szimmetrikus, és előjelük jelzi a jobb- és baloldali aszimmetriát.
A Pearson-féle A mutató:
x−Mo A =
σ
A számtani átlag és a módusz értékének azonossága esetén a mutató értéke 0, ami jelzi a szimmetriát. A
mutató pozitív előjele a jobb oldali, negatív előjele a bal oldali aszimmetriát mutatja. A mutatónak nincs
felső korlátja, tehát a mutatószám értéke nem utal közvetlenül az aszimmetria mértékére.
Az aszimmetria mérésére szolgáló F-mutató:
X
32