Numerical Methods Contents - SAM

0 50 100 150 200 250 300 350 400 450 500
page rank
0.1
0.09
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
step 5
page rank
0.1
0.09
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
step 15
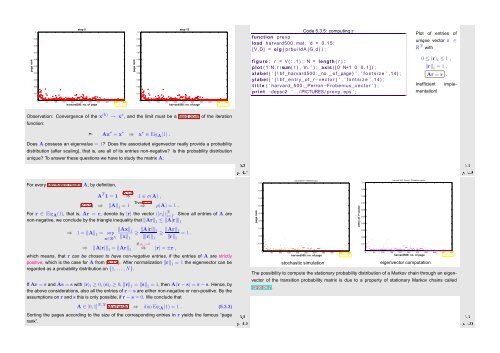
1 function prevp
Code 5.3.5: computing r
2 load harvard500 . mat ; d = 0 . 1 5 ;
3 [ V,D] = eig ( p r b u i l d A (G, d ) ) ;
4
5 figure ; r = V ( : , 1 ) ; N = length ( r ) ;
6 plot ( 1 :N, r /sum( r ) , ’m. ’ ) ; axis ( [ 0 N+1 0 0 . 1 ] ) ;
7 xlabel ( ’ { \ b f harvard500 : no . o f page } ’ , ’ f o n t s i z e ’ ,14) ;
8 ylabel ( ’ { \ b f e n t r y o f r−vector } ’ , ’ f o n t s i z e ’ ,14) ;
9 t i t l e ( ’ harvard 500: Perron−Frobenius vector ’ ) ;
10 p r i n t −depsc2 ’ . . / PICTURES/ prevp . eps ’ ;
Plot of entries of
unique vector r ∈
R N with
0 ≤ (r) i ≤ 1 ,
‖r‖ 1 = 1 ,
Inefficient
Ar = r .
implementation!
0
harvard500: no. of page
Fig. 62
0
200 250 300 350
harvard500: no. of page
450 500
Fig. 63
0 50 100 150 400
Observation: Convergence of the x (k) → x ∗ , and the limit must be a fixed point of the iteration
function:
➣ Ax ∗ = x ∗ ⇒ x ∗ ∈ Eig A (1) .
Does A possess an eigenvalue = 1? Does the associated eigenvector really provide a probability
distribution (after scaling), that is, are all of its entries non-negative? Is this probability distribution
unique? To answer these questions we have to study the matrix A:
Ôº½ º¿
Ôº½ º¿
For every stochastic matrix A, by definition,
A T 1 = 1 (5.1.2)
⇒ 1 ∈ σ(A) ,
(2.5.5) ⇒ ‖A‖ 1 = 1
Thm 5.1.2
⇒ ρ(A) = 1 .
For r ∈ Eig A (1), that is, Ar = r, denote by |r| the vector (|r i |) N i=1 . Since all entries of A are
non-negative, we conclude by the triangle inequality that ‖Ar‖ 1 ≤ ‖A|r|‖ 1
⇒
1 = ‖A‖ 1 = sup
x∈R N ‖Ax‖ 1
‖x‖ 1
≥ ‖A|r|‖ 1
‖|r|‖ 1
≥ ‖Ar‖ 1
‖r‖ 1
= 1 .
⇒ ‖A|r|‖ 1 = ‖Ar‖ 1
if a ij >0
⇒ |r| = ±r ,
which means, that r can be chosen to have non-negative entries, if the entries of A are strictly
positive, which is the case for A from (5.3.2). After normalization ‖r‖ 1 = 1 the eigenvector can be
regarded as a probability distribution on {1,...,N}.
If Ar = r and As = s with (r) i ≥ 0, (s) i ≥ 0, ‖r‖ 1 = ‖s‖ 1 = 1, then A(r − s) = r − s. Hence, by
the above considerations, also all the entries of r − s are either non-negative or non-positive. By the
assumptions on r and s this is only possible, if r − s = 0. We conclude that
A ∈ ]0, 1] N,N stochastic ⇒ dim Eig A (1) = 1 . (5.3.3)
Sorting the pages according to the size of the corresponding entries in r yields the famous “page
rank”.
Ôº½ º¿
page rank
0.09
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
harvard500: 1000000 hops
0
200 250 300 350
harvard500: no. of page
450 500
Fig. 64
0 50 100 150 400
stochastic simulation
entry of r−vector
0.1
0.09
0.08
0.07
0.06
0.05
0.04
0.03
0.02
0.01
harvard 500: Perron−Frobenius vector
0
200 250 300 350
harvard500: no. of page
450 500
Fig. 65
0 50 100 150 400
eigenvector computation
The possibility to compute the stationary probability distribution of a Markov chain through an eigenvector
of the transition probability matrix is due to a property of stationary Markov chains called
ergodicity.
Ôº¾¼ º¿