Numerical Methods Contents - SAM

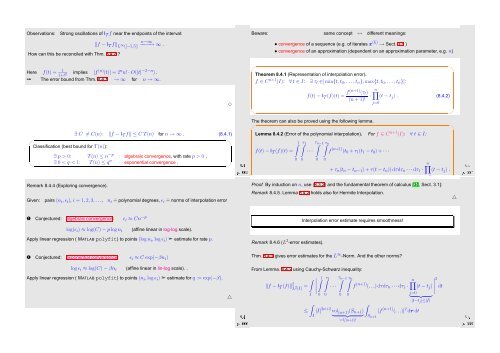
Observations:
Strong oscillations of I T f near the endpoints of the interval:
‖f − I T f‖ L ∞ (]−5,5[)
How can this be reconciled with Thm. 8.4.2 ?
n→∞
−−−−→ ∞ .
Beware: same concept ↔ different meanings:
• convergence of a sequence (e.g. of iterates x (k) → Sect. 3.1 )
• convergence of an approximation (dependent on an approximation parameter, e.g. n)
Here f(t) = 1
1+t 2 implies |f (n) (t)| = 2 n n! · O(|t| −2−n ) .
➙ The error bound from Thm. 8.4.1 → ∞ for n → ∞.
✬
Theorem 8.4.1 (Representation of interpolation error).
f ∈ C n+1 (I): ∀ t ∈ I: ∃ τ t ∈] min{t,t 0 , ...,t n }, max{t,t 0 , ...,t n }[:
✩
✸
f(t) − I T (f)(t) = f(n+1) (τ t )
(n + 1)!
·
n∏
(t − t j ) . (8.4.2)
j=0
✫
✪
The theorem can also be proved using the following lemma.
✬
✩
✬
Classification (best bound for T(n)):
✫
∃ C ≠ C(n): ‖f − I T f‖ ≤ C T(n) for n → ∞ . (8.4.1)
∃ p > 0: T(n) ≤ n −p : algebraic convergence, with rate p > 0 ,
✩
º ✪
∃ 0 < q < 1: T(n) ≤ q n : exponential convergence .
Ôº
Remark 8.4.4 (Exploring convergence).
Given: pairs (n i , ǫ i ), i = 1, 2, 3,..., n i ˆ= polynomial degrees, ǫ i ˆ= norms of interpolation error
Lemma 8.4.2 (Error of the polynomial interpolation). For f ∈ C n+1 (I): ∀ t ∈ I:
∫1 ∫ 1 ∫
f(t) − I T (f)(t) = · · ·
0 0τ
0
✫
τ n−1∫
n
0τ
f (n+1) (t 0 + τ 1 (t 1 − t 0 ) + · · ·
n∏
+ τ n (t n − t n−1 ) + τ(t − t n )) dτdτ n · · · dτ 1 ·
j=0
Ôº º
(t − t j ) .
Proof. By induction on n, use (8.3.2) and the fundamental theorem of calculus [34, Sect. 3.1]:
Remark 8.4.5. Lemma 8.4.2 holds also for Hermite Interpolation.
△
✪
➊ Conjectured: algebraic convergence: ǫ i ≈ Cn −p
log(ǫ i ) ≈ log(C) − p log n i (affine linear in log-log scale).
Apply linear regression ( MATLAB polyfit) to points (log n i , log ǫ i ) ➣ estimate for rate p.
➊ Conjectured: exponential convergence: ǫ i ≈ C exp(−βn i )
Remark 8.4.6 (L 2 -error estimates).
Interpolation error estimate requires smoothness!
Thm. 8.4.1 gives error estimates for the L ∞ -Norm. And the other norms?
log ǫ i ≈ log(C) − βn i (affine linear in lin-log scale). .
Apply linear regression ( MATLAB polyfit) to points (n i , log ǫ i ) ➣ estimate for q := exp(−β).
△
Ôº º
From Lemma. 8.4.2 using Cauchy-Schwarz inequality:
∫
∫1 ∫ τ 1 τ∫
n−1 ∫ τ n
‖f − I T (f)‖ 2 L 2 (I) = n∏
2
· · · f (n+1) (...) dτdτ
∣
n · · · dτ 1 · (t − t j )
dt
∣
I 0 0 0 0
j=0
} {{ }
|t−t j |≤|I|
∫
≤
I
∫
|I| 2n+2 vol (n+1) (S n+1 ) |f (n+1) (...)| 2 dτ dt
} {{ } S n+1
=1/(n+1)!
Ôº º