Numerical Methods Contents - SAM

x 2
a
.
x 1
Q =
x 2
( ) cosϕ sinϕ
− sinϕ cosϕ
a
ϕ x
. 1
• Practice: for the sake of numerical stability (in order to avoid so-called cancellation) choose
{ 12 (a + ‖a‖
v =
2 e 1 ) , if a 1 > 0 ,
1
2 (a − ‖a‖ 2 e 1) , if a 1 ≤ 0 .
However, this is not really needed [24, Sect. 19.1] !
• If K = C and a 1 = |a 1 | exp(iϕ), ϕ ∈ [0, 2π[, then choose
v = 1 2 (a ± ‖a‖ 2 e 1 exp(−iϕ)) in (2.8.2).
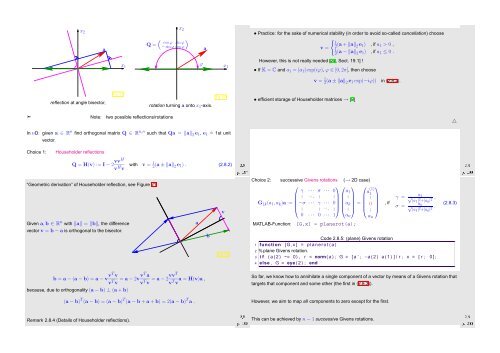
reflection at angle bisector,
Fig. 21
rotation turning a onto x 1 -axis.
Fig. 22
• efficient storage of Householder matrices → [2]
➣ Note: two possible reflections/rotations
△
In nD: given a ∈ R n find orthogonal matrix Q ∈ R n,n such that Qa = ‖a‖ 2 e 1 , e 1 ˆ= 1st unit
Choice 1:
vector.
Householder reflections
Q = H(v) := I − 2 vvH
v H v with v = 1 2 (a ± ‖a‖ 2 e 1) . (2.8.2)
Ôº½
¾º
Ôº½ ¾º
“Geometric derivation” of Householder reflection, see Figure 21
Given a,b ∈ R n with ‖a‖ = ‖b‖, the difference
vector v = b − a is orthogonal to the bisector.
a
b
v
Fig. 23
Choice 2: successive Givens rotations (→ 2D case)
⎛
⎞⎛
⎞ ⎛
¯γ · · · ¯σ · · · 0 a 1 a (1) ⎞
. ... . .
.
1 G 1k (a 1 , a k )a :=
⎜−σ · · · γ · · · 0
⎟⎜a k
⎟
⎝ . . . .. . ⎠⎝
. ⎠ = .
γ =
⎜ ⎟
⎝
0. ⎠ , if σ =
0 · · · 0 · · · 1 a n a n
MATLAB-Function:
[G,x] = planerot(a);
a 1 √|a1
| 2 +|a k | 2 ,
√|a1
a k
| 2 +|a k | . (2.8.3)
2
Code 2.8.5: (plane) Givens rotation
1 function [G, x ] = p l a n e r o t ( a )
2 % plane Givens rotation.
3 i f ( a ( 2 ) ~= 0) , r = norm( a ) ; G = [ a ’ ; −a ( 2 ) a ( 1 ) ] / r ; x = [ r ; 0 ] ;
4 else , G = eye ( 2 ) ; end
b = a − (a − b) = a − v vT v
v T v = a − 2vvT a
v T v = a − 2vvT v T v a = H(v)a ,
because, due to orthogonality (a − b) ⊥ (a + b)
So far, we know how to annihilate a single component of a vector by means of a Givens rotation that
targets that component and some other (the first in (2.8.3)).
(a − b) T (a − b) = (a − b) T (a − b + a + b) = 2(a − b) T a .
Remark 2.8.4 (Details of Householder reflections).
Ôº½ ¾º
However, we aim to map all components to zero except for the first.
This can be achieved by n − 1 successive Givens rotations.
Ôº¾¼¼ ¾º