Numerical Methods Contents - SAM

The previous example (Code 2.8.14) showed that assembly of the Q-factor in the QR-factorization
of A is not needed, when the linear system of equations Ax = b is to be solved by means of QRfactorization:
the orthogonal transformations can simply be applied to the right hand side(s) whenever
they are applied to the columns of A.
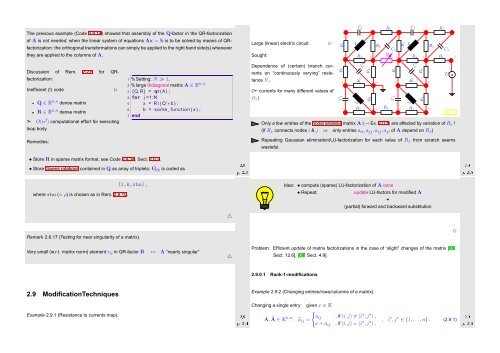
Large (linear) electric circuit
Sought:
✄
R1
L
C 1
R 4
R 2
R 1
C 1 R 1
C 2
R1
L
R 2
C 2
15 16 R 4 7 R 1
17
Discussion of Rem. 2.2.6 for QRfactorization:
Inefficient (!) code
✄
Q ∈ R n,n dense matrix
R ∈ R n,n dense matrix
➣ O(n 2 ) computational effort for executing
loop body
1 % Setting: N ≫ 1,
2 % large tridiagonal matrix A ∈ R n,n
3 [Q,R] = qr (A) ;
4 for j =1:N
5 x = R \ ( Q’∗b) ;
6 b = some_function ( x ) ;
7 end
Dependence of (certain) branch currents
on “continuously varying” resistance
R x
(➣ currents for many different values of
R x )
R1
C1
R2
8 18
9 10
L
C2
R3
R4
R x
Fig. 26
L
R 2
R 2 R2
11 12 13 14
Only a few entries of the nodal analysis matrix A (→ Ex. 2.0.1) are affected by variation of R x !
(If R x connects nodes i & j ⇒ only entries a ii , a jj ,a ij , a ji of A depend on R x )
R1
C1
R2
C2
R3
R4
U
~
Remedies:
• Store R in sparse matrix format, see Code 2.8.14, Sect. 2.6.2.
• Store Givens rotations contained in Q as array of triplets: G lk is coded as
Ôº¾½¿ ¾º
Repeating Gaussian elimination/LU-factorization for each value of R x from scratch seems
wasteful.
Ôº¾½ ¾º
where rho (ˆ= ρ) is chosen as in Rem. 2.8.10.
[l,k,rho] ,
△
Idea: • compute (sparse) LU-factorization of A once
• Repeat:
update LU-factors for modified A
+
(partial) forward and backward substitution
Remark 2.8.17 (Testing for near singularity of a matrix).
Very small (w.r.t. matrix norm) element r ii in QR-factor R ↔ A “nearly singular”
△
Problem: Efficient update of matrix factorizations in the case of ‘slight” changes of the matrix [18,
Sect. 12.6], [38, Sect. 4.9].
✸
2.9.0.1 Rank-1-modifications
2.9 ModificationTechniques
Example 2.9.2 (Changing entries/rows/columns of a matrix).
Example 2.9.1 (Resistance to currents map).
Ôº¾½ ¾º
Changing a single entry: given x ∈ K
{
A,Ã ∈ Kn,n a
: ã ij = ij , if (i,j) ≠ (i ∗ , j ∗ ) ,
x + a ij , if (i,j) = (i ∗ , j ∗ ) ,
Ôº¾½ ¾º
, i ∗ ,j ∗ ∈ {1, ...,n} . (2.9.1)