Numerical Methods Contents - SAM

0 500 1000 1500 2000 2500 3000
x low frequency power spectrum
104
14
12
0.6
0.4
m−1 ∑
h m−k = y 2j + iy 2j+1 ωm
j(m−k)
j=0
= ∑ m−1
j=0 y 2j ω jk
m − i ·
∑ m−1
j=0 y 2j+1 ω jk
m . (7.2.10)
|c k
| 2
10
8
6
sound pressure
0.2
0
−0.2
⇒
∑ m−1
j=0 y 2j ω jk
m = 1 2 (h k + h m−k ) ,
Use simple identities for roots of unity:
∑ m−1
j=0 y 2j+1 ω jk
m = − 1 2 i(h k − h m−k ) .
4
2
0
index k of Fourier coefficient
−0.4
−0.6
Sampled signal
cutt−off = 1000
cutt−off = 3000
cutt−off = 5000
−0.8
0.68 0.69 0.7 0.71 0.72 0.73 0.74
time[s]
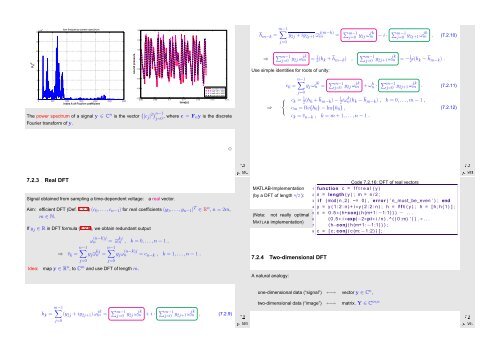
The power spectrum of a signal y ∈ C n is the vector ( |c j | 2) n−1
j=0 , where c = F ny is the discrete
Fourier transform of y.
⇒
n−1 ∑
c k = y j ωn jk = ∑ m−1
j=0 y 2j ωm jk + ωn k ·
j=0
∑ m−1
j=0 y 2j+1 ω jk
m . (7.2.11)
{ ck = 1 2 (h k + h m−k ) − 1 2 iωk n(h k − h m−k ) , k = 0,...,m − 1 ,
c m = Re{h 0 } − Im{h 0 } ,
c k = c n−k , k = m + 1,...,n − 1 .
(7.2.12)
✸
Ôº½ º¾
Ôº¿ º¾
7.2.3 Real DFT
Signal obtained from sampling a time-dependent voltage:
a real vector.
Aim: efficient DFT (Def. 7.2.3) (c 0 , . ..,c n−1 ) for real coefficients (y 0 ,...,y n−1 ) T ∈ R n , n = 2m,
m ∈ N.
If y j ∈ R in DFT formula (7.2.8), we obtain redundant output
n−1 ∑
⇒ c k =
j=0
ω (n−k)j
n
y j ω kj
n =
= ω kj
n , k = 0, ...,n − 1 ,
n−1 ∑
y j ω n (n−k)j = c n−k , k = 1,...,n − 1 .
j=0
MATLAB-Implementation
(by a DFT of length n/2 ):
(Note:
not really optimal
MATLAB implementation)
7.2.4 Two-dimensional DFT
Code 7.2.16: DFT of real vectors
1 function c = f f t r e a l ( y )
2 n = length ( y ) ; m = n / 2 ;
3 i f (mod( n , 2 ) ~= 0) , error ( ’ n must be even ’ ) ; end
4 y = y ( 1 : 2 : n ) + i ∗y ( 2 : 2 : n ) ; h = f f t ( y ) ; h = [ h ; h ( 1 ) ] ;
5 c = 0.5∗( h+conj ( h (m+1: −1:1) ) ) − . . .
6 (0.5∗ i ∗exp(−2∗pi∗ i / n ) . ^ ( ( 0 :m) ’ ) ) . ∗ . . .
7 ( h−conj ( h (m+1: −1:1) ) ) ;
8 c = [ c ; conj ( c (m: −1:2) ) ] ;
Idea: map y ∈ R n , to C m and use DFT of length m.
A natural analogy:
one-dimensional data (“signal”) ←→ vector y ∈ C n ,
m−1 ∑
h k = (y 2j + iy 2j+1 ) ωm jk = ∑ m−1
j=0 y 2j ωm jk + i ·
j=0
∑ m−1
Ôº¾ º¾
j=0 y 2j+1 ωm jk , (7.2.9)
two-dimensional data (“image”) ←→ matrix. Y ∈ C m,n
Ôº º¾