Numerical Methods Contents - SAM

121 x = ( a : ( b−a ) / 1 0 0 : b ) ;
122 pb = ( ya ∗(b−x ) .^2 + 2∗w∗( x−a ) . ∗ ( b−x ) +yb ∗( x−a ) . ^ 2 ) / ( ( b−a ) ^2) ;
123 plot ( x , pb , ’ r−’ , ’ l i n e w i d t h ’ ,2) ;
124
125 plot ( p ( j ) , ya , ’ go ’ ) ;
126 end
127
128 % replot initial nodes over the other plots:
129 plot ( t , y , ’ k∗ ’ ) ;
130 % plot(p,yb,’go’)
131 legend ( [ h p l o t ( 1 ) , h p l o t s l ( 1 ) , h p l o t ( 2 : 4 ) ] , leg ) ;
132 t i t l e ( ’ Shape preserving i n t e r p o l a t i o n ’ )
A proof of Weierstrass approximation theorem (see [9, Sect. 6.2]):
✬
Theorem 9.5.1 (Approximation by Bernstein polynomials). If f ∈ C([0, 1]) and
p n (t) := ∑ ( )
n n
j=0 f(j/n) t j (1 − t) n−j , 0 ≤ t ≤ 1 ,
j
then p n → f uniformly for n → ∞. When f ∈ C m ([0, 1]), then p (k)
n → f (k) , 0 ≤ k ≤ m,
uniformly for n → ∞.
✫
Example 9.5.1 (Bernstein approximation).
{
0 , if |2t − 1| > 1 f 1 (t) :=
2 ,
1
1
2 (1 + cos(2π(2t − 1))) otherwise , f 2 (t) :=
1 + e −12(x−1/2) .
✩
✪
9.5 Bezier Techniques
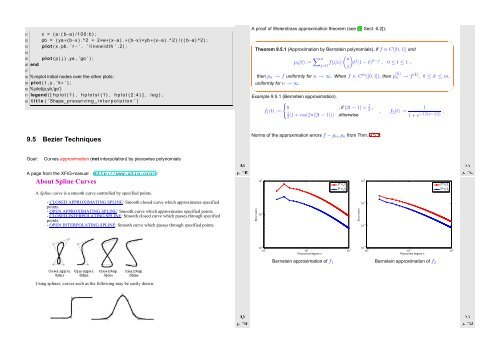
Norms of the approximation errors f − p n , p n from Thm. 9.5.1:
Ôº º
Goal: Curves approximation (not interpolation) by piecewise polynomials
A page from the XFIG-manual (http://www.xfig.org/):
About Spline Curves
||f−p n
|| ∞
||f−p n
|| ∞
Ôº½ º
A Spline curve is a smooth curve controlled by specified points.
||f−p n
|| 2
||f−p n
|| 2
- CLOSED APPROXIMATING SPLINE: Smooth closed curve which approximates specified
points.
- OPEN APPROXIMATING SPLINE: Smooth curve which approximates specified points.
- CLOSED INTERPOLATING SPLINE: Smooth closed curve which passes through specified
points.
- OPEN INTERPOLATING SPLINE: Smooth curve which passes through specified points.
Error norm
10 0 Polynomial degree n
10 −1
Error norm
10 0 Polynomial degree n
10 −1
10 −2
10 −2
10 −3
10 0 10 1 10 2
Bernstein approximation of f 1 Bernstein approximation of f 2
10 0 10 1 10 2
Using splines, curves such as the following may be easily drawn.
Ôº¼ º
Ôº¾ º