Numerical Methods Contents - SAM

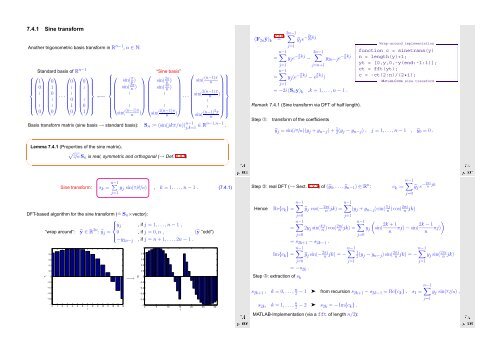
7.4.1 Sine transform
Another trigonometric basis transform in R n−1 , n ∈ N:
Standard basis of R n−1 ⎧
⎧⎛
⎞⎛
⎞ ⎛ ⎞⎛
⎞⎫
⎛
1 0
⎪⎨
1
0.
0.
· · ·
0..
⎪⎬ ⎪⎨
⎜ ⎟⎜
⎟ ⎜0
⎟⎜.
←−
⎟ ⎜
⎝.
⎠⎝
0.. ⎠ ⎝1⎠⎝0⎠
⎝
⎪⎩
0 0 0 1
⎪⎭ ⎪⎩
sin( π n )
sin( 2π n )
.
.
sin( (n−1)π
n )
Basis transform matrix (sine basis → standard basis):
“Sine basis”
⎞⎛
sin( 2π ⎞ ⎛ ⎞⎫
n )
sin( 4π n )
sin( (n−1)π
n
.
· · ·
sin( 2(n−1)π
n )
⎪⎬
⎟
⎠⎜
⎝ .
⎟
.
⎠ ⎜
sin( 2(n−1)π ⎝ . ⎟
⎠
n ) sin( (n−1)2 π ⎪⎭
n
S n := (sin(jkπ/n)) n−1
j,k=1 ∈ Rn−1,n−1 .
2n−1
(7.2.8)
∑
(F 2n ỹ) k = ỹ j e −2π 2n kj
j=1
n−1 ∑
= y j e −π n kj −
2n−1 ∑
j=1 j=n+1
n−1 ∑
= y j (e −π n kj − en πkj )
y 2n−j e −π n kj
j=1
= −2i (S n y) k ,k = 1,...,n − 1 .
Remark 7.4.1 (Sine transform via DFT of half length).
Step ➀:
transform of the coefficients
Wrap-around implementation
function c = sinetrans(y)
n = length(y)+1;
yt = [0,y,0,-y(end:-1:1)];
ct = fft(yt);
c = -ct(2:n)/(2*i);
MATLAB-CODE sine transform
ỹ j = sin(jπ/n)(y j + y n−j ) + 1 2 (y j − y n−j ) , j = 1, . ..,n − 1 , ỹ 0 = 0 .
✬
Lemma 7.4.1 (Properties of the sine matrix).
√ 2 /nS n is real, symmetric and orthogonal (→ Def. 2.8.1)
✫
✩
Ôº¼ º
✪
Ôº¼ º
Sine transform:
s k = n−1 ∑
y j sin(πjk/n) , k = 1,...,n − 1 . (7.4.1)
j=1
DFT-based algorithm for the sine transform (ˆ= S n ×vector):
⎧
⎪⎨ y j , if j = 1, ...,n − 1 ,
“wrap around”: ỹ ∈ R 2n : ỹ j = 0 , if j = 0, n , (ỹ “odd”)
⎪⎩
−y 2n−j , if j = n + 1, ...,2n − 1 .
y j
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
j
−→
tyj
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
0 5 10 15 20 25 30
j
Ôº¼ º
n−1
Step ➁: real DFT (→ Sect. 7.2.3) of (ỹ 0 ,...,ỹ n−1 ) ∈ R n ∑
: c k := ỹ j e −2πi n jk
n−1 ∑
n−1
Hence Re{c k } = ỹ j cos(− 2πi
n jk) = ∑
(y j + y n−j ) sin( πj
n ) cos(2πi n jk)
j=0
j=1
n−1 ∑
= 2y j sin( πj
n−1
n ) cos(2πi n jk) = ∑
(
y j sin( 2k + 1
)
− 1
πj) − sin(2k
n n πj) j=0
j=0
= s 2k+1 − s 2k−1 .
n−1 ∑
n−1
Im{c k } = ỹ j sin(− 2πi
n jk) = − ∑
n−1
1
2 (y j − y n−j ) sin( 2πi
n jk) = − ∑
j=0
j=1
j=1
= −s 2k .
Step ➂: extraction of s k
j=0
y j sin( 2πi
n jk)
n−1
s 2k+1 , k = 0, ..., n 2 − 1 ➤ from recursion s ∑
2k+1 − s 2k−1 = Re{c k } , s 1 = y j sin(πj/n) ,
s 2k , k = 1, ..., n 2 − 2 ➤ s 2k = − Im{c k } .
MATLAB-Implementation (via a fft of length n/2):
j=1
Ôº¼ º