Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
0 20 40 60 80 100<br />
0<br />
20<br />
0<br />
20<br />
0<br />
20<br />
Definition 2.7.1 (Symmetric positive definite (s.p.d.) matrices).<br />
M ∈ K n,n , n ∈ N, is symmetric (Hermitian) positive definite (s.p.d.), if<br />
40<br />
40<br />
40<br />
M = M H ∧ x H Mx > 0 ⇔ x ≠ 0 .<br />
60<br />
60<br />
60<br />
If x H Mx ≥ 0 for all x ∈ K n ✄ M positive semi-definite.<br />
80<br />
80<br />
80<br />
100<br />
100<br />
100<br />
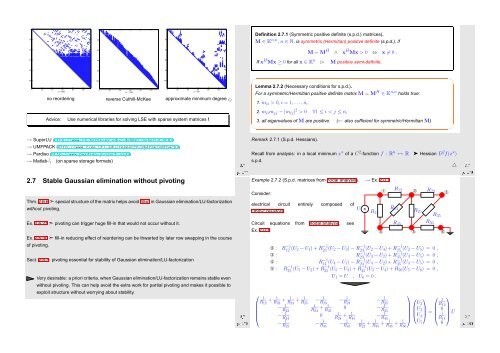
nz = 2580<br />
0 20 40 60 80 100<br />
0 20 40 60 80 100<br />
nz = 891<br />
nz = 1299<br />
no reordering<br />
reverse Cuthill-McKee approximate minimum degree ✸<br />
Advice: Use numerical libraries for solving LSE with sparse system matrices !<br />
✬<br />
Lemma 2.7.2 (Necessary conditions for s.p.d.).<br />
For a symmetric/Hermitian positive definite matrix M = M H ∈ K n,n holds true:<br />
1. m ii > 0, i = 1, ...,n,<br />
2. m ii m jj − |m ij | 2 > 0 ∀1 ≤ i < j ≤ n,<br />
3. all eigenvalues of M are positive. (← also sufficient for symmetric/Hermitian M)<br />
✫<br />
✩<br />
✪<br />
→ SuperLU (http://www.cs.berkeley.edu/~demmel/SuperLU.html)<br />
→ UMFPACK (http://www.cise.ufl.edu/research/sparse/umfpack/)<br />
→ Pardiso<br />
Ôº½ ¾º<br />
(http://www.pardiso-project.org/)<br />
→ Matlab-\ (on sparse storage formats)<br />
2.7 Stable Gaussian elimination without pivoting<br />
Remark 2.7.1 (S.p.d. Hessians).<br />
Recall from analysis: in a local minimum x ∗ of a C 2 -function f : R n ↦→ R ➤ Hessian D 2 f(x ∗ )<br />
s.p.d.<br />
Example 2.7.2 (S.p.d. matrices from nodal analysis). → Ex. 2.0.1<br />
△<br />
Ôº½ ¾º<br />
Thm. 2.6.6 ➣ special structure of the matrix helps avoid fill-in in Gaussian elimination/LU-factorization<br />
without pivoting.<br />
Consider:<br />
electrical circuit entirely composed of<br />
Ohmic resistors.<br />
U<br />
➀<br />
R 12 ➁ R 23 ➂<br />
~ R 24<br />
R 14<br />
R 25<br />
R 35<br />
Ex. 2.6.21 ➣ pivoting can trigger huge fill-in that would not occur without it.<br />
Ex. 2.6.30 ➣ fill-in reducing effect of reordering can be thwarted by later row swapping in the course<br />
of pivoting.<br />
Sect. 2.5.3: pivoting essential for stability of Gaussian elimination/LU-factorization<br />
Very desirable: a priori criteria, when Gaussian elimination/LU-factorization remains stable even<br />
without pivoting. This can help avoid the extra work for partial pivoting and makes it possible to<br />
exploit structure without worrying about stability.<br />
Ôº½ ¾º<br />
Circuit equations from nodal analysis, see<br />
Ex. 2.0.1:<br />
R45<br />
R 56<br />
➃ ➄ ➅<br />
➁ : R12 −1 (U 2 − U 1 ) + R23 −1 (U 2 − U 3 ) − R24 −1 (U 2 − U 4 ) + R25 −1 (U 2 − U 5 ) = 0 ,<br />
➂ :<br />
R23 −1 (U 3 − U 2 ) + R35 −1 (U 3 − U 5 ) = 0 ,<br />
➃ :<br />
R14 −1 (U 4 − U 1 ) − R24 −1 (U 4 − U 2 ) + R45 −1 (U 4 − U 5 ) = 0 ,<br />
➄ : R25 −1 (U 5 − U 2 ) + R35 −1 (U 5 − U 3 ) + R45 −1 (U 5 − U 4 ) + R 56 (U 5 − U 6 ) = 0 ,<br />
U 1 = U , U 6 = 0 .<br />
⎛<br />
1<br />
R + 12 R 1 + 23 R 1 + 24 R 1 − 25 R 1 − 23 R 1<br />
− 1 ⎞<br />
⎛ ⎞ ⎛ ⎞<br />
1<br />
24 R 25<br />
− R 1<br />
1<br />
23 R + 1<br />
23 R 0 − 1<br />
U 2 R 35 R 35<br />
⎜<br />
⎝ −R 1<br />
0 1<br />
24 R + 1<br />
24 R − 1<br />
⎜U 3<br />
12<br />
⎟<br />
⎟ ⎝<br />
45 R 45 ⎠<br />
U 4 ⎠ = 0<br />
⎜<br />
⎝<br />
1 ⎟<br />
−R 1<br />
− 1<br />
25 R − 1 1<br />
35 R 45 R + 1<br />
22 R + 1<br />
35 R + 1<br />
R ⎠ U<br />
14<br />
U 5 0<br />
45 R 56<br />
Ôº½¼ ¾º