Numerical Methods Contents - SAM

Ax = b :
1 LU-decomposition A = LU, #elementary operations 1 3n(n − 1)(n + 1)
2 forward substitution, solve Lz = b, #elementary operations 1 2n(n − 1)
3 backward substitution, solve Ux = z, #elementary operations 1 2n(n + 1)
(in leading order) the same as for Gaussian elimination
Remark 2.2.6 (Many sequential solutions of LSE).
With A 11 ∈ K n,n regular, A 12 ∈ K n,m , A 21 ∈ K m,n , A 22 ∈ K m,m :
( ) ( ) ( )
A11 A 12 I 0 A11 A Schur complement
=
12
A 21 A 22 A 21 A −1
,
11 I 0 S S := A 22 − A 21 A −1
11 A 12
→ block Gaussian elimination, see Rem. 2.1.4.
(2.2.2)
△
Given:
regular matrix A ∈ K n,n , n ∈ N, and N ∈ N, both n,N large
foolish !
1 % Setting: N ≫ 1, large matrix A
2 for j =1:N
3 x = A\ b ;
4 b = some_function ( x ) ;
5 end
computational effort O(Nn 3 )
smart !
1 % Setting: N ≫ 1, large matrix A
2 [ L ,U] = lu (A) ;
3 for j =1:N
4 x = U \ ( L \ b ) ;
5 b = some_function ( x ) ;
6 end
Ôº¿ ¾º¾
+ N backward substitutions (cost Nn 2 )
computational effort O(n 3 + Nn 2 )
Efficient implementation requires one LU-decomposition of A (cost O(n 3 )) + N forward substitutions
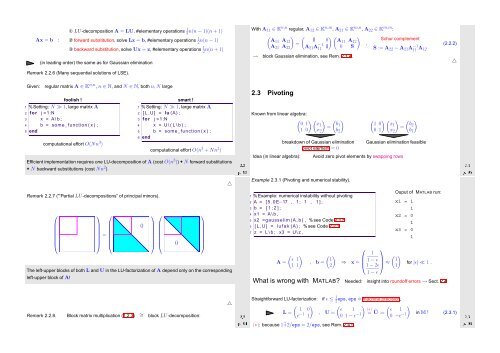
Remark 2.2.7 ("‘Partial LU-decompositions” of principal minors).
⎛
⎜
⎝
⎞
⎛
=
⎟ ⎜
⎠ ⎝
0
⎞ ⎛
⎟ ⎜
⎠ ⎝ 0
The left-upper blocks of both L and U in the LU-factorization of A depend only on the corresponding
left-upper block of A!
⎞
⎟
⎠
△
2.3 Pivoting
Known from linear algebra:
( ) ( ) ( ) ( )( ) ( )
0 1 x1 b1
1 0 x1 b2
= =
1 0 x 2 b 2 0 1 x 2 b 1
Idea (in linear algebra):
breakdown of Gaussian elimination
pivot element = 0
Example 2.3.1 (Pivoting and numerical stability).
1 % Example: numerical instability without pivoting
2 A = [ 5 . 0 E−17 , 1 ; 1 , 1 ] ;
3 b = [ 1 ; 2 ] ;
4 x1 = A \ b ,
5 x2 =gausselim (A, b ) , % see Code 2.1.5
6 [ L ,U] = l u f a k (A) ; % see Code 2.2.1
7 z = L \ b ; x3 = U\ z ,
A =
( )
ǫ 1
1 1
Gaussian elimination feasible
Avoid zero pivot elements by swapping rows
(
1
, b =
2)
⎛
⇒ x = ⎜
⎝
1
1 − ǫ
1 − 2ǫ
1 − ǫ
⎞
( )
⎟ 1
⎠ ≈ 1
Ouput of MATLAB run:
x1 = 1
1
x2 = 0
1
x3 = 0
1
for |ǫ| ≪ 1 .
What is wrong with MATLAB? Needed: insight into roundoff errors → Sect. 2.4
Ôº ¾º¿
△
Remark 2.2.8. Block matrix multiplication (1.2.3) ∼ = block LU-decomposition:
Ôº ¾º¾
Straightforward LU-factorization: if ǫ ≤ 1 2eps,eps ˆ= machine precision,
( ) ( ) ( )
1 0 ǫ 1 (∗) ǫ 1
L =
ǫ −1 , U =
1 0 1 − ǫ −1 = Ũ := 0 −ǫ −1
(∗): because 1˜+2/eps = 2/eps, see Rem. 2.4.9.
in M ! (2.3.1)
Ôº ¾º¿