Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
You also want an ePaper? Increase the reach of your titles
YUMPU automatically turns print PDFs into web optimized ePapers that Google loves.
ootstrapping = use the same idea in a simpler version to get y(t 0 + c i h), noting that these values<br />
can be replaced by other approximations obtained by methods already constructed (this approach<br />
will be elucidated in the next example).<br />
1<br />
0.9<br />
0.8<br />
0.7<br />
y(t)<br />
Explicit Euler<br />
Explicit trapezoidal rule<br />
Explicit midpoint rule<br />
10 −1<br />
s=1, Explicit Euler<br />
s=2, Explicit trapezoidal rule<br />
s=2, Explicit midpoint rule<br />
O(h 2 )<br />
What error can we afford in the approximation of y(t 0 +c i h) (under the assumption that f is Lipschitz<br />
continuous)?<br />
y<br />
0.6<br />
0.5<br />
0.4<br />
0.3<br />
error |y h<br />
(1)−y(1)|<br />
10 −2<br />
10 −3<br />
0.2<br />
10 −4<br />
Goal: one-step error y(t 1 ) − y 1 = O(h p+1 )<br />
0.1<br />
0<br />
0 0.2 0.4 0.6 0.8 1<br />
t<br />
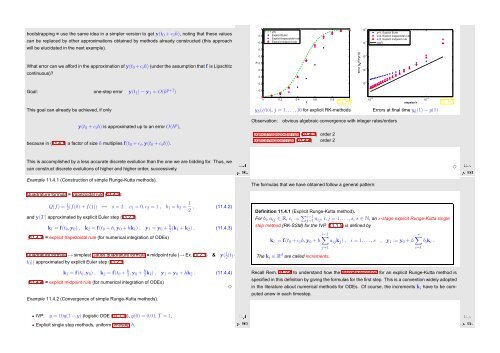
Fig. 142<br />
10 0 stepsize h<br />
10 −2 10 −1<br />
Fig. 143<br />
This goal can already be achieved, if only<br />
y h (j/10), j = 1,...,10 for explicit RK-methods<br />
Errors at final time y h (1) − y(1)<br />
y(t 0 + c i h) is approximated up to an error O(h p ),<br />
because in (11.4.1) a factor of size h multiplies f(t 0 + c i ,y(t 0 + c i h)).<br />
Observation:<br />
obvious algebraic convergence with integer rates/orders<br />
explicit trapezoidal rule (11.4.3) order 2<br />
explicit midpoint rule (11.4.4) order 2<br />
This is accomplished by a less accurate discrete evolution than the one we are bidding for. Thus, we<br />
can construct discrete evolutions of higher and higher order, successively.<br />
Ôº½ ½½º<br />
Ôº¿ ½½º ✸<br />
Example 11.4.1 (Construction of simple Runge-Kutta methods).<br />
The formulas that we have obtained follow a general pattern:<br />
Quadrature formula = trapezoidal rule (11.4.2):<br />
Q(f) = 1 2 (f(0) + f(1)) ↔ s = 2: c 1 = 0,c 2 = 1 , b 1 = b 2 = 1 2 , (11.4.2)<br />
and y(T) approximated by explicit Euler step (11.2.1)<br />
k 1 = f(t 0 ,y 0 ) , k 2 = f(t 0 + h,y 0 + hk 1 ) , y 1 = y 0 + h 2 (k 1 + k 2 ) . (11.4.3)<br />
(11.4.3) = explicit trapezoidal rule (for numerical integration of ODEs)<br />
Quadrature formula → simplest Gauss quadrature formula = midpoint rule (→ Ex. 10.2.1) & y( 1 2 (t 1+<br />
t 0 )) approximated by explicit Euler step (11.2.1)<br />
Definition 11.4.1 (Explicit Runge-Kutta method).<br />
For b i ,a ij ∈ R, c i := ∑ i−1<br />
j=1 a ij, i,j = 1, ...,s, s ∈ N, an s-stage explicit Runge-Kutta single<br />
step method (RK-SSM) for the IVP (11.1.5) is defined by<br />
∑i−1<br />
s∑<br />
k i := f(t 0 + c i h,y 0 + h a ij k j ) , i = 1, ...,s , y 1 := y 0 + h b i k i .<br />
j=1<br />
The k i ∈ R d are called increments.<br />
i=1<br />
k 1 = f(t 0 ,y 0 ) , k 2 = f(t 0 + h 2 ,y 0 + h 2 k 1) , y 1 = y 0 + hk 2 . (11.4.4)<br />
(11.4.4) = explicit midpoint rule (for numerical integration of ODEs)<br />
✸<br />
Example 11.4.2 (Convergence of simple Runge-Kutta methods).<br />
IVP: ẏ = 10y(1 − y) (logistic ODE (11.1.1)), y(0) = 0.01, T = 1,<br />
Explicit single step methods, uniform timestep h.<br />
Ôº¾ ½½º<br />
Recall Rem. 11.2.4 to understand how the discrete evolution for an explicit Runge-Kutta method is<br />
specified in this definition by giving the formulas for the first step. This is a convention widely adopted<br />
in the literature about numerical methods for ODEs. Of course, the increments k i have to be computed<br />
anew in each timestep.<br />
Ôº ½½º