Numerical Methods Contents - SAM

10
9
Remark 9.3.9 (Non-linear interpolation).
8
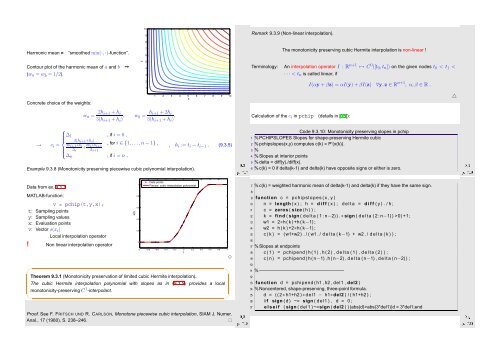
Harmonic mean =
“smoothed min(·, ·)-function”.
7
6
The monotonicity preserving cubic Hermite interpolation is non-linear !
Contour plot of the harmonic mean of a and b ➙
(w a = w b = 1/2).
b
5
4
3
Terminology: An interpolation operator I : R n+1 ↦→ C 0 ([t 0 , t n ]) on the given nodes t 0 < t 1 <
· · · < t n is called linear, if
2
1
I(αy + βz) = αI(y) + βI(z) ∀y,z ∈ R n+1 , α, β ∈ R .
Concrete choice of the weights:
1 2 3 4 5 6 7 8 9 10
a
△
w a = 2h i+1 + h i
3(h i+1 + h i ) , w b = h i+1 + 2h i
3(h i+1 + h i ) ,
⎧
∆ 1 , if i = 0 ,
⎪⎨ 3(h i+1 +h i )
→ c i = 2h i+1 +h i
∆ + 2h i +h , for i ∈ {1, ...,n − 1} ,
i+1
i ∆ i+1 ⎪⎩
∆ n , if i = n ,
Example 9.3.8 (Monotonicity preserving piecewise cubic polynomial interpolation).
, h i := t i − t i−1 . (9.3.5)
Ôº½ º¿
Calculation of the c i in pchip (details in [15]):
Code 9.3.10: Monotonicity preserving slopes in pchip
1 % PCHIPSLOPES Slopes for shape-preserving Hermite cubic
2 % pchipslopes(x,y) computes c(k) = P’(x(k)).
3 %
Ôº½ º¿
4 % Slopes at interior points
5 % delta = diff(y)./diff(x).
6 % c(k) = 0 if delta(k-1) and delta(k) have opposite signs or either is zero.
Data from ex. 9.1.1
MATLAB-function:
v = pchip(t,y,x);
t: Sampling points
y: Sampling values
x: Evaluation points
v: Vector s(x i )
Local interpolation operator
! Non linear interpolation operator
✬
✫
s(t)
1
0.8
0.6
0.4
0.2
0
Data points
Piecew. cubic interpolation polynomial
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
t
Theorem 9.3.1 (Monotonicity preservation of limited cubic Hermite interpolation).
The cubic Hermite interpolation polynomial with slopes as in (9.3.5) provides a local
monotonicity-preserving C 1 -interpolant.
Proof. See F. FRITSCH UND R. CARLSON, Monotone piecewise cubic interpolation, SIAM J. Numer.
Anal., 17 (1980), S. 238–246.
✸
✩
✪
Ôº½ º¿
7 % c(k) = weighted harmonic mean of delta(k-1) and delta(k) if they have the same sign.
8
9 function c = pchipslopes ( x , y )
10 n = length ( x ) ; h = d i f f ( x ) ; d e l t a = d i f f ( y ) . / h ;
11 c = zeros ( size ( h ) ) ;
12 k = find ( sign ( d e l t a ( 1 : n−2) ) .∗ sign ( d e l t a ( 2 : n−1) ) >0) +1;
13 w1 = 2∗h ( k ) +h ( k−1) ;
14 w2 = h ( k ) +2∗h ( k−1) ;
15 c ( k ) = (w1+w2) . / ( w1 . / d e l t a ( k−1) + w2 . / d e l t a ( k ) ) ;
16
17 % Slopes at endpoints
18 c ( 1 ) = pchipend ( h ( 1 ) , h ( 2 ) , d e l t a ( 1 ) , d e l t a ( 2 ) ) ;
19 c ( n ) = pchipend ( h ( n−1) , h ( n−2) , d e l t a ( n−1) , d e l t a ( n−2) ) ;
20
21 % ——————————————————-
22
23 function d = pchipend ( h1 , h2 , del1 , del2 )
24 % Noncentered, shape-preserving, three-point formula.
25 d = ( ( 2∗h1+h2 ) ∗del1 − h1∗del2 ) / ( h1+h2 ) ;
26 i f sign ( d ) ~= sign ( del1 ) , d = 0 ;
27 e l s e i f ( sign ( del1 ) ~=sign ( del2 ) ) (abs(d)>abs(3*del1))d = 3*del1;end
Ôº¾¼ º