Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
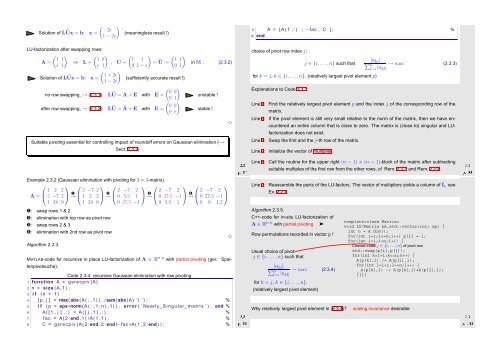
Solution of LŨx = b: x<br />
( )<br />
2ǫ<br />
= 1 − 2ǫ<br />
(meaningless result !)<br />
9 A = [A ( 1 , : ) ; −fac , C ] ; %<br />
10 end<br />
LU-factorization after swapping rows:<br />
( ) ( ) (<br />
1 1<br />
1 0 1 1<br />
A = ⇒ L = , U =<br />
ǫ 1 ǫ 1 0 1 − ǫ<br />
Solution of LŨx = b: x<br />
= (<br />
1 + 2ǫ<br />
1 − 2ǫ<br />
)<br />
)<br />
( )<br />
1 1<br />
= Ũ := 0 1<br />
(sufficiently accurate result !)<br />
( )<br />
0 0<br />
no row swapping, → (2.3.1): LŨ = A + E with E = 0 1<br />
( )<br />
0 0<br />
after row swapping, → (2.3.2): LŨ = Ã + E with E = 0 ǫ<br />
in M . (2.3.2)<br />
unstable !<br />
stable !<br />
Suitable pivoting essential for controlling impact of roundoff errors on Gaussian elimination (→<br />
Sect. 2.5.2)<br />
✸<br />
Ôº ¾º¿<br />
choice of pivot row index j:<br />
j ∈ {i,...,n} such that<br />
for k = j, k ∈ {i,...,n}. (relatively largest pivot element p)<br />
Explanations to Code 2.3.3:<br />
|a ki |<br />
∑ nl=i<br />
|a kl|<br />
→ max (2.3.3)<br />
Line 4: Find the relatively largest pivot element p and the index j of the corresponding row of the<br />
matrix.<br />
Line 5: If the pivot element is still very small relative to the norm of the matrix, then we have encountered<br />
an entire column that is close to zero. The matrix is (close to) singular and LUfactorization<br />
does not exist.<br />
Line 6: Swap the first and the j-th row of the matrix.<br />
Line 7: Initialize the vector of multiplier.<br />
Line 8: Call the routine for the upper right (n − 1) × (n − 1)-block of the matrix after subtracting<br />
suitable multiples of the first row from the other rows, cf. Rem. 2.1.3 and Rem. 2.2.4.<br />
Ôº ¾º¿<br />
Example 2.3.2 (Gaussian elimination with pivoting for 3 × 3-matrix).<br />
⎛<br />
A = ⎝ 1 2 2<br />
⎞ ⎛<br />
2 −7 2 ⎠ →<br />
➊ ⎝ 2 −7 2<br />
⎞ ⎛<br />
1 2 2 ⎠ →<br />
➋ ⎝ 2 −7 2<br />
⎞ ⎛<br />
0 5.5 1 ⎠ →<br />
➌ ⎝ 2 −7 2<br />
⎞ ⎛<br />
0 27.5 −1 ⎠ →<br />
➍ ⎝ 2 −7 2<br />
⎞<br />
0 27.5 −1 ⎠<br />
1 24 0 1 24 0 0 27.5 −1 0 5.5 1 0 0 1.2<br />
➊: swap rows 1 & 2.<br />
➋: elimination with top row as pivot row<br />
➌: swap rows 2 & 3<br />
➍: elimination with 2nd row as pivot row<br />
Algorithm 2.3.3.<br />
MATLAB-code for recursive in place LU-factorization of A ∈ R n,n with partial pivoting (ger.: Spaltenpivotsuche):<br />
Code 2.3.4: recursive Gaussian elimination with row pivoting<br />
1 function A = gsrecpiv (A)<br />
2 n = size (A, 1 ) ;<br />
3 i f ( n > 1)<br />
4 [ p , j ] = max( abs (A ( : , 1 ) ) . / sum( abs (A) ’ ) ’ ) ; %<br />
Ôº ¾º¿<br />
5 i f ( p < eps∗norm(A ( : , 1 : n ) ,1) ) , error ( ’ Nearly Singular m a trix ’ ) ; end %<br />
6 A ( [ 1 , j ] , : ) = A ( [ j , 1 ] , : ) ; %<br />
7 fac = A( 2 : end , 1 ) / A( 1 , 1 ) ; %<br />
8 C = gsrecpiv (A ( 2 : end , 2 : end )−fac∗A( 1 , 2 : end ) ) ; %<br />
✸<br />
Line 9: Reassemble the parts of the LU-factors. The vector of multipliers yields a column of L, see<br />
Ex. 2.2.1.<br />
Algorithm 2.3.5.<br />
C++-code for in-situ LU-factorization of<br />
A ∈ R n,n with partial pivoting ➤<br />
Row permutations recorded in vector p !<br />
Usual choice of pivot:<br />
j ∈ {i, ...,n} such that<br />
|a ki |<br />
∑ nl=i<br />
|a kl|<br />
→ max (2.3.4)<br />
for k = j, k ∈ {i,...,n}.<br />
(relatively largest pivot element)<br />
Why relatively largest pivot element in (2.3.4)?<br />
template<br />
void LU(Matrix &A,std::vector &p) {<br />
int n = A.dim();<br />
for(int i=1;i