Numerical Methods Contents - SAM

In other words, roundoff errors may badly affect the length of the solution w, but not its direction.
Practice: If, in the course of Gaussian elimination/LU-factorization a zero pivot element is really encountered,
then we just replace it with eps, in order to avoid inf values!
Thm. 5.3.2 ➣ Convergence of shifted inverse iteration for A H = A:
Asymptotic linear convergence, Rayleigh quotient → λ j with rate
|λ j − α|
min{|λ i − α|, i ≠ j} with λ j ∈ σ(A) , |α − λ j | ≤ |α − λ| ∀λ ∈ σ(A) .
Idea:
Extremely fast for α ≈ λ j !
Algorithm 5.3.16 (Rayleigh quotient iteration).
Rayleigh
quotient
iteration
(for normal A ∈ K n,n )
preserves sparsity,
Sect. 2.6.2
see
A posteriori adaptation of shift
Use α := ρ A (z (k−1) ) in k-th step of inverse iteration.
MATLAB-CODE : Rayleigh quotient iteration
function [z,lmin] = rqui(A,tol,maxit)
alpha = 0; n = size(A,1);
z = rand(size(A,1),1); z = z/norm(z);
for i=1:maxit
z = (A-alpha*speye(n))\z;
z = z/norm(z); lmin=dot(A*z,z);
if (abs(alpha-lmin) < tol), break; end;
alpha = lmin;
end
△
(5.3.17)
Ôº½ º¿
10 −5
10 −10
10 −15
1 2 3 4 5 6 7 8 9 10
10 0 k
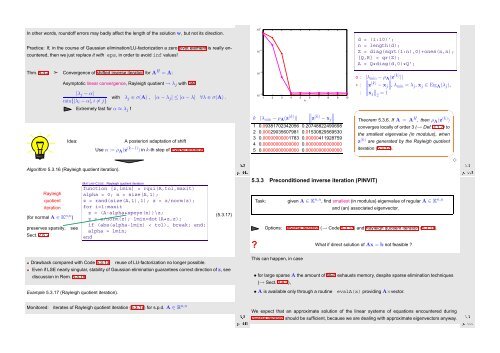
k |λ min − ρ A (z (k) )|
∥
∥z (k) − x j
∥ ∥∥
1 0.09381702342056 0.20748822490698
2 0.00029035607981 0.01530829569530
3 0.00000000001783 0.00000411928759
4 0.00000000000000 0.00000000000000
5 0.00000000000000 0.00000000000000
d = (1:10)’;
n = length(d);
Z = diag(sqrt(1:n),0)+ones(n,n);
[Q,R] = qr(Z);
A = Q*diag(d,0)*Q’;
o : |λ min − ρ A ∥(z (k) )|
∥
∗ : ∥z (k) ∥∥,
− x j λmin = λ j , x j ∈ Eig A (λ j ),
∥ ∥
: ∥x ∥2 j = 1
✬
Theorem 5.3.6. If A = A H , then ρ A (z (k) )
converges locally of order 3 (→ Def. 3.1.7) to
the smallest eigenvalue (in modulus), when
z (k) are generated by the Rayleigh quotient
iteration (5.3.17).
✫
5.3.3 Preconditioned inverse iteration (PINVIT)
Task:
given A ∈ K n,n , find smallest (in modulus) eigenvalue of regular A ∈ K n,n
and (an) associated eigenvector.
Options: inverse iteration (→ Code 5.3.13) and Rayleigh quotient iteration (5.3.17).
? What if direct solution of Ax = b not feasible ?
✩
Ôº¿ º¿
✪
✸
Drawback compared with Code 5.3.13: reuse of LU-factorization no longer possible.
Even if LSE nearly singular, stability of Gaussian elimination guarantees correct direction of z, see
discussion in Rem. 5.3.15.
This can happen, in case
• for large sparse A the amount of fill-in exhausts memory, despite sparse elimination techniques
(→ Sect. 2.6.3),
Example 5.3.17 (Rayleigh quotient iteration).
• A is available only through a routine
evalA(x) providing A×vector.
Monitored:
iterates of Rayleigh quotient iteration (5.3.17) for s.p.d. A ∈ R n,n
Ôº¾ º¿
We expect that an approximate solution of the linear systems of equations encountered during
inverse iteration should be sufficient, because we are dealing with approximate eigenvectors anyway.
Ôº º¿