Numerical Methods Contents - SAM

Algebraic order of convergence in h = min { 1 + regularity of f, 4 }.
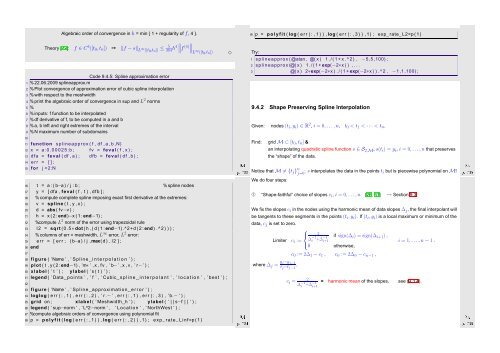
39 p = p o l y f i t ( log ( e r r ( : , 1 ) ) , log ( e r r ( : , 3 ) ) ,1) ; exp_rate_L2=p ( 1 )
Theory [22]: f ∈ C 4 ([t 0 , t n ]) ➙ ‖f − s‖ L ∞ ([t 0 ,t n ]) ≤ 5
384 h4 ∥ ∥ ∥f
(4) ∥ ∥ ∥L ∞ ([t 0 ,t n ]) ✸
Code 9.4.5: Spline approximation error
1 % 22.06.2009 splineapprox.m
2 % Plot convergence of approximation error of cubic spline interpolation
3 % with respect to the meshwidth
4 % print the algebraic order of convergence in sup and L 2 norms
5 %
6 % inputs: f function to be interpolated
7 % df derivative of f, to be computed in a and b
8 % a, b left and right extremes of the interval
9 % N maximum number of subdomains
10
11 function splineapprox ( f , df , a , b ,N)
12 x = a :0.00025:b ; f v = feval ( f , x ) ;
Ôº¿¿ º
13 dfa = feval ( df , a ) ; dfb = feval ( df , b ) ;
14 e r r = [ ] ;
15 for j =2:N
16 t = a : ( b−a ) / j : b ; % spline nodes
17 y = [ dfa , feval ( f , t ) , dfb ] ;
18 % compute complete spline imposing exact first derivative at the extremes:
19 v = spline ( t , y , x ) ;
20 d = abs ( fv−v ) ;
21 h = x ( 2 : end )−x ( 1 : end−1) ;
22 %compute L 2 norm of the error using trapezoidal rule
23 l 2 = sqrt (0.5∗ dot ( h , ( d ( 1 : end−1).^2+d ( 2 : end ) . ^ 2 ) ) ) ;
24 % columns of err = meshwidth, L ∞ error, L 2 error:
25 e r r = [ e r r ; ( b−a ) / j ,max( d ) , l 2 ] ;
26 end
27
28 figure ( ’Name ’ , ’ Spline i n t e r p o l a t i o n ’ ) ;
29 plot ( t , y ( 2 : end−1) , ’m∗ ’ , x , fv , ’ b−’ , x , v , ’ r−’ ) ;
30 xlabel ( ’ t ’ ) ; ylabel ( ’ s ( t ) ’ ) ;
31 legend ( ’ Data p o i n t s ’ , ’ f ’ , ’ Cubic s p l i n e i n t e r p o l a n t ’ , ’ l o c a t i o n ’ , ’ best ’ ) ;
32
33 figure ( ’Name ’ , ’ Spline approximation e r r o r ’ ) ;
34 loglog ( e r r ( : , 1 ) , e r r ( : , 2 ) , ’ r .− ’ , e r r ( : , 1 ) , e r r ( : , 3 ) , ’ b.− ’ ) ;
35 grid on ; xlabel ( ’ Meshwidth h ’ ) ; ylabel ( ’ | | s−f | | ’ ) ;
Ôº¿ º
36 legend ( ’ sup−norm ’ , ’ L^2−norm ’ , ’ Location ’ , ’ NorthWest ’ ) ;
37 %compute algebraic orders of convergence using polynomial fit
38 p = p o l y f i t ( log ( e r r ( : , 1 ) ) , log ( e r r ( : , 2 ) ) ,1) ; e xp_rate_Linf=p ( 1 )
Try:
1 splineapprox ( @atan , @( x ) 1 . / ( 1 + x . ^ 2 ) , −5 ,5 ,100) ;
2 splineapprox (@( x ) 1 . / ( 1 + exp(−2∗x ) ) , . . .
3 @( x ) 2∗exp(−2∗x ) . / ( 1 + exp(−2∗x ) ) . ^ 2 , −1 ,1 ,100) ;
9.4.2 Shape Preserving Spline Interpolation
Given: nodes (t i ,y i ) ∈ R 2 , i = 0,...,n, t 0 < t 1 < · · · < t n .
Find:
grid M ⊂ [t 0 , t n ] &
an interpolating quadratic spline function s ∈ S 2,M , s(t i ) = y i , i = 0,...,n that preserves
the “shape” of the data.
Notice that M ≠ {t j } n j=0 : s interpolates the data in the points t i but is piecewise polynomial on M!
We do four steps:
➀ “Shape-faithful” choice of slopes c i , i = 0,...,n [26, 31] → Section 9.3
We fix the slopes c i in the nodes using the harmonic mean of data slopes ∆ j , the final interpolant will
be tangents to these segments in the points (t i ,y i ). If (t i , y i ) is a local maximum or minimum of the
data, c j is set to zero.
⎧
⎨ 2
Limiter c i := ∆ −1
i +∆ −1 if sign(∆ i ) = sign(∆ i+1 ) ,
i+1
⎩0 otherwise,
where ∆ j = y j−y j−1
t j −t j−1
.
c 0 := 2∆ 1 − c 1 , c n := 2∆ n − c n−1 ,
c i = 2
∆ −1
i +∆ −1
i+1
i = 1, ...,n − 1 .
= harmonic mean of the slopes, see (9.3.4).
Ôº¿ º
Ôº¿ º