Numerical Methods Contents - SAM

(x (k) ) k∈N0 Cauchy sequence ➤ convergent x (k) k→∞
−−−−→ x ∗ . .
Continuity of Φ ➤ Φ(x ∗ ) = x ∗ . Uniqueness of fixed point is evident. ✷
△
Φ(x)
Φ(x)
A simple criterion for a differentiable Φ to be contractive:
✬
✩
x
x
Lemma 3.2.4 (Sufficient condition for local linear convergence of fixed point iteration).
If Φ : U ⊂ R n ↦→ R n , Φ(x ∗ ) = x ∗ ,Φ differentiable in x ∗ , and ‖DΦ(x ∗ )‖ < 1, then the fixed
point iteration (3.2.1) converges locally and at least linearly.
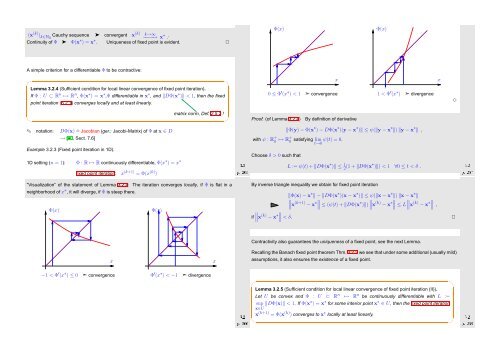
0 ≤ Φ ′ (x ∗ ) < 1 ➣ convergence
1 < Φ ′ (x ∗ ) ➣ divergence
✸
✫
matrix norm, Def. 2.5.2 !
✪
Proof. (of Lemma 3.2.4)
By definition of derivative
✎ notation: DΦ(x) ˆ= Jacobian (ger.: Jacobi-Matrix) of Φ at x ∈ D
→ [40, Sect. 7.6]
Example 3.2.3 (Fixed point iteration in 1D).
1D setting (n = 1):
Ôº¾ ¿º¾
Φ : R ↦→ R continuously differentiable, Φ(x ∗ ) = x ∗
fixed point iteration: x (k+1) = Φ(x (k) )
with ψ : R + 0 ↦→ R+ 0
Choose δ > 0 such that
‖Φ(y) − Φ(x ∗ ) − DΦ(x ∗ )(y − x ∗ )‖ ≤ ψ(‖y − x ∗ ‖) ‖y − x ∗ ‖ ,
satisfying lim ψ(t) = 0.
t→0
L := ψ(t) + ‖DΦ(x ∗ )‖ ≤ 1 2 (1 + ‖DΦ(x∗ )‖) < 1 ∀0 ≤ t < δ .
Ôº¾ ¿º¾
“Visualization” of the statement of Lemma 3.2.4: The iteration converges locally, if Φ is flat in a
neighborhood of x ∗ , it will diverge, if Φ is steep there.
Φ(x)
Φ(x)
By inverse triangle inequality we obtain for fixed point iteration
‖Φ(x) − x ∗ ‖ − ‖DΦ(x ∗ )(x − x ∗ )‖ ≤ ψ(‖x − x ∗ ‖) ‖x − x ∗ ‖
∥
∥x (k+1) − x ∗∥ ∥ ≤ (ψ(t) + ‖DΦ(x ∗ ∥
)‖) ∥x (k) − x ∗∥ ∥
∥ ∥∥x ≤ L (k) − x ∗∥ ∥ ,
∥
if ∥x (k) − x ∗∥ ∥ < δ.
✷
Contractivity also guarantees the uniqueness of a fixed point, see the next Lemma.
x
x
Recalling the Banach fixed point theorem Thm. 3.2.3 we see that under some additional (usually mild)
assumptions, it also ensures the existence of a fixed point.
−1 < Φ ′ (x ∗ ) ≤ 0 ➣ convergence
Φ ′ (x ∗ ) < −1 ➣ divergence
✬
✩
Ôº¾ ¿º¾
Lemma 3.2.5 (Sufficient condition for local linear convergence of fixed point iteration (II)).
Let U be convex and Φ : U ⊂ R n ↦→ R n be continuously differentiable with L :=
sup ‖DΦ(x)‖ < 1. If Φ(x ∗ ) = x ∗ for some interior point x ∗ ∈ U, then the fixed point iteration
x∈U
x (k+1) = Φ(x (k) ) converges to x ∗ locally at least linearly.
✫
Ôº¾ ¿º¾
✪