Numerical Methods Contents - SAM

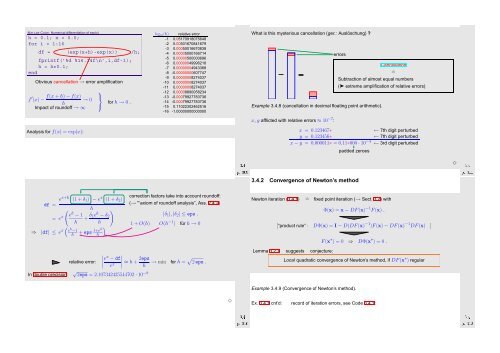
MATLAB-CODE: Numerical differentiation of exp(x)
log 10 (h) relative error
h = 0.1; x = 0.0;
-1 0.05170918075648
for i = 1:16
-2 0.00501670841679
-3 0.00050016670838
df = (exp(x+h)-exp(x)) /h;
-4 0.00005000166714
-5 0.00000500000696
fprintf(’%d %16.14f\n’,i,df-1);
-6 0.00000049996218
h = h*0.1;
-7 0.00000004943368
end
-8 -0.00000000607747
-9 0.00000008274037
Obvious cancellation → error amplification
-10 0.00000008274037
-11 0.00000008274037
⎫
-12 0.00008890058234
f ′ f(x + h) − f(x) ⎬
-13 -0.00079927783736
(x) − → 0
h
Impact of roundoff → ∞ ⎭ for h → 0 . -14 -0.00079927783736
-15 0.11022302462516
-16 -1.00000000000000
What is this mysterious cancellation (ger.: Auslöschung) ?
errors
Cancellation
ˆ=
Subtraction of almost equal numbers
(➤ extreme amplification of relative errors)
Example 3.4.8 (cancellation in decimal floating point arithmetic).
x, y afflicted with relative errors ≈ 10 −7 :
Analysis for f(x) = exp(x):
x = 0.123467∗
← 7th digit perturbed
y = 0.123456∗
← 7th digit perturbed
x − y = 0.000011∗ = 0.11∗000 · 10 −4 ← 3rd digit perturbed
Ôº¿¼ ¿º
padded zeroes
Ôº¿½½ ¿º
✸
3.4.2 Convergence of Newton’s method
⇒
e x+h (1 + δ 1 ) − e x (1 + δ 2 )
df =
( h )
= e x e h − 1
+ δ 1e h − δ 2
(
h h
)
|df| ≤ e x e h −1
h +eps 1+eh
h
correction factors take into account roundoff:
(→ "‘axiom of roundoff analysis”, Ass. 2.4.2)
|δ 1 |, |δ 2 | ≤ eps .
1 + O(h) O(h −1 ) für h → 0
Newton iteration (3.4.1) ˆ= fixed point iteration (→ Sect. 3.2) with
Φ(x) = x − DF(x) −1 F(x) .
[“product rule” : DΦ(x) = I − D(DF(x) −1 )F(x) − DF(x) −1 DF(x) ]
F(x ∗ ) = 0 ⇒ DΦ(x ∗ ) = 0 .
relative error:
e x ∣
−df ∣∣∣
∣ e x ≈ h + 2eps
h → min for h = √ 2eps .
√
In double precision: 2eps = 2.107342425544702 · 10 −8
Lemma 3.2.7 suggests conjecture:
Local quadratic convergence of Newton’s method, if DF(x ∗ ) regular
Example 3.4.9 (Convergence of Newton’s method).
✸
Ôº¿½¼ ¿º
Ex. 3.4.1 cnt’d: record of iteration errors, see Code 3.4.1:
Ôº¿½¾ ¿º