Numerical Methods Contents - SAM

Thus, iterative solvers for solving Aw = z (k−1) may be considered, see Sect. 4. However, the
required accuracy is not clear a priori. Here we examine an approach that completely dispenses with
an iterative solver and uses a preconditioner (→ Def. 4.3.1) instead.
Idea:
(for inverse iteration without shift, A = A H s.p.d.)
Instead of solving Aw = z (k−1) compute w = B −1 z (k−1) with
“inexpensive” s.p.d. approximate inverse B −1 ≈ A −1
➣ B ˆ= Preconditioner for A, see Def. 4.3.1
Code 5.3.18: preconditioned inverse iteration (5.3.18)
1 function [ lmin , z , res ] = p i n v i t ( evalA , n , invB , t o l , maxit )
2 z = ( 1 : n ) ’ ; z = z / norm( z ) ; res = [ ] ; rho = 0 ;
3 for i =1: maxit
4 v = evalA ( z ) ; rhon = dot ( v , z ) ; r = v − rhon∗z ;
5 z = z − invB ( r ) ; z = z / norm( z ) ; res = [ res ; rhon ] ;
6 i f ( abs ( rho−rhon ) < t o l ∗abs ( rhon ) ) , break ;
7 else rho = rhon ; end
8 end
9 lmin = dot ( evalA ( z ) , z ) ; res = [ res ; lmin ] ,
Example 5.3.19 (Convergence of PINVIT).
Computational
effort:
1 matrix×vector
1 evaluation of
preconditioner
A
few
AXPY-operations
!
Possible to replace A −1 with B −1 in inverse iteration ?
NO, because we are not interested in smallest eigenvalue of B !
Replacement A −1 → B −1 possible only when applied to residual quantity
residual quantity = quantity that → 0 in the case of convergence to exact solution
Ôº º¿
S.p.d. matrix A ∈ R n,n , tridiagonal preconditioner, see Ex. 4.3.4
1 A = spdiags ( repmat ( [ 1 / n, −1 ,2∗(1+1/n ) , −1 ,1/n ] , n , 1 ) ,[−n/2 , −1 ,0 ,1 ,n / 2 ] , n , n ) ;
2 evalA = @( x ) A∗x ;
3 % inverse iteration
4 invB = @( x ) A \ x ;
5 % tridiagonal preconditioning
6 B = spdiags ( spdiags (A,[ − 1 ,0 ,1]) ,[ −1 ,0 ,1] , n , n ) ; invB = @( x ) B \ x ;
Ôº º¿
Natural residual quantity for eigenvalue problem Ax = λx:
r := Az − ρ A (z)z , ρ A (z) = Rayleigh quotient → Def. 5.3.1 .
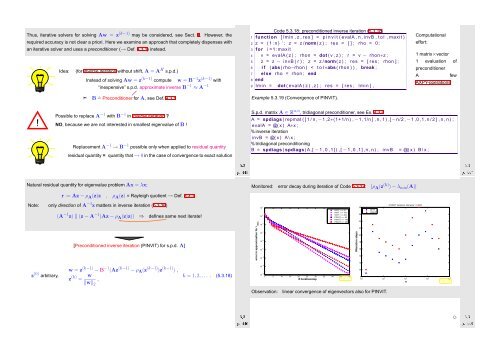
Monitored: error decay during iteration of Code 5.3.17: |ρ A (z (k) ) − λ min (A)|
Note: only direction of A −1 z matters in inverse iteration (5.3.16)
(A −1 z) ‖ (z − A −1 (Az − ρ A (z)z)) ⇒ defines same next iterate!
[Preconditioned inverse iteration (PINVIT) for s.p.d. A]
error in approximation for λ max
10 0
10 −2
10 −4
10 −6
10 −8
10 −10
INVIT, n = 50
INVIT, n = 100
INVIT, n = 200
PINVIT, n = 50
PINVIT, n = 100
PINVIT, n = 200
#iteration steps
28
26
24
22
20
18
16
14
INVIT
PINVIT
(P)INVIT iterations: tolerance = 0.0001
12
z (0) arbitrary,
w = z (k−1) − B −1 (Az (k−1) − ρ A (z (k−1) )z (k−1) ) ,
z (k) =
w ,
‖w‖ 2
k = 1, 2,... . (5.3.18)
10 2 # iterationstep
10 −12
10 −14
0 5 10 15 20 25 30 35 40 45 50
10
8
Fig. 71 10 1 10 2 10 3 10 4 10 5
n
Fig. 72
Observation:
linear convergence of eigenvectors also for PINVIT.
Ôº º¿
Ôº º¿ ✸