Numerical Methods Contents - SAM

8 end
9 t1 = min ( t1 , toc ) ;
10 end
11 [ I , J ] = meshgrid ( 0 : n−1 ,0:n−1) ; F = exp(−2∗pi∗ i ∗ I .∗ J / n ) ;
12 t2 = realmax ; for k =1:5 , t i c ; c = F∗y ; t2 = min ( t2 , toc ) ; end
13 t3 = realmax ; for k =1:5 , t i c ; d = f f t ( y ) ; t3 = min ( t3 , toc ) ; end
14 res = [ res ; n t1 t2 t3 ] ;
15 end
16
17 figure ( ’name ’ , ’FFT t i m i n g ’ ) ;
18 semilogy ( res ( : , 1 ) , res ( : , 2 ) , ’ b−’ , res ( : , 1 ) , res ( : , 3 ) , ’ k−’ ,
res ( : , 1 ) , res ( : , 4 ) , ’ r−’ ) ;
19 ylabel ( ’ { \ b f run time [ s ] } ’ , ’ Fontsize ’ ,14) ;
20 xlabel ( ’ { \ b f vector l e n g th n } ’ , ’ Fontsize ’ ,14) ;
21 legend ( ’ loop based computation ’ , ’ d i r e c t m a trix m u l t i p l i c a t i o n ’ , ’MATLAB
f f t ( ) f u n c t i o n ’ ,1) ;
22 p r i n t −deps2c ’ . . / PICTURES/ f f t t i m e . eps ’
Ôº¿ º¿
The secret of MATLAB’s fft():
the Fast Fourier Transform algorithm [14]
(discovered by C.F. Gauss in 1805, rediscovered by Cooley & Tuckey in 1965,
one of the “top ten algorithms of the century”).
An elementary manipulation of (7.2.8) for n = 2m, m ∈ N:
Note m-periodicity:
n−1 ∑
c k = y j e −2πi n jk
=
j=0
m−1 ∑
m−1
y 2j e −2πi n 2jk ∑
+
j=0
m−1 ∑
= y 2j e −2πi m
} {{ jk }
j=0 =ωm
} {{ jk
}
=:˜c even
k
˜c even
k
= ˜c even
k+m ,
˜codd k
j=0
+e −2πi n k ·
= ˜c odd
k+m .
y 2j+1 e −2πi n (2j+1)k
m−1 ∑
y 2k+1 e −2πi m
} {{ jk }
j=0 =ωm
} {{ jk
}
=:˜c odd
k
.
(7.3.1)
Ôº º¿
MATLAB-CODE naive DFT-implementation
c = zeros(n,1);
omega = exp(-2*pi*i/n);
c(1) = sum(y); s = omega;
for j=2:n
c(j) = y(n);
for k=n-1:-1:1
c(j) = c(j)*s+y(k);
end
s = s*omega;
end
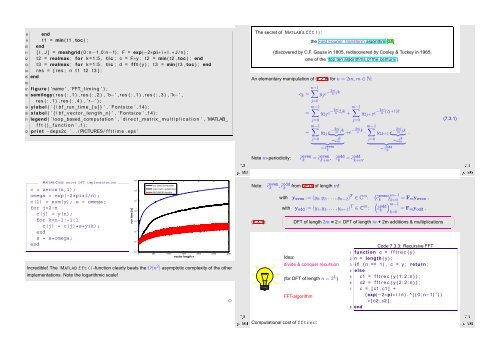
run time [s]
10 1
10 0
10 −1
10 −2
10 −3
10 −4
10 −5
10 −6
loop based computation
direct matrix multiplication
MATLAB fft() function
0 500 1000 1500 2000 2500 3000
vector length n
Incredible! The MATLAB fft()-function clearly beats the O(n 2 ) asymptotic complexity of the other
implementations. Note the logarithmic scale!
✸
Ôº º¿
Note:
(7.3.1):
˜c even
k
, ˜c odd
k
from DFTs of length m!
with y even := (y 0 , y 2 ,...,y n−2 ) T ∈ C m :
with y odd := (y 1 , y 3 ,...,y n−1 ) T ∈ C m :
✗
✖
Idea:
(˜c
even) m−1
k k=0 = F my even ,
( ) m−1
˜c odd
k = F my odd .
k=0
DFT of length 2m = 2× DFT of length m + 2m additions & multiplications
divide & conquer recursion
(for DFT of length n = 2 L )
FFT-algorithm
Computational cost of fftrec:
Code 7.3.3: Recursive FFT
1 function c = f f t r e c ( y )
2 n = length ( y ) ;
3 i f ( n == 1) , c = y ; return ;
4 else
5 c1 = f f t r e c ( y ( 1 : 2 : n ) ) ;
6 c2 = f f t r e c ( y ( 2 : 2 : n ) ) ;
7 c = [ c1 ; c1 ] +
( exp(−2∗pi∗ i / n ) . ^ ( ( 0 : n−1) ’ ) )
. ∗ [ c2 ; c2 ] ;
8 end
✔
✕
Ôº º¿