Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Numerical Methods Contents - SAM
Create successful ePaper yourself
Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.
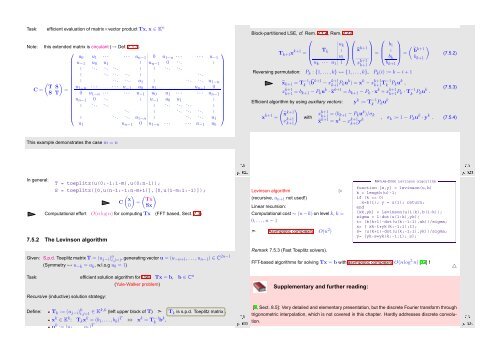
Task:<br />
efficient evaluation of matrix×vector product Tx, x ∈ K n<br />
Note: this extended matrix is circulant (→ Def. 7.1.3)<br />
⎛<br />
⎞<br />
u 0 u 1 · · · · · · u n−1 0 u 1−n · · · · · · u −1<br />
u −1 u 0 u 1 . u n−1 0 . .. .<br />
. . .. ... . .. . . ... . ..<br />
. ... . .. ... . . ..<br />
( )<br />
. . .. ... u 1 . ... . .. u 1−n<br />
T S<br />
u<br />
C = =<br />
1−n · · · · · · u −1 u 0 u 1 u n−1 0<br />
S T<br />
0 u 1−n · · · · · · u −1 u 0 u 1 · · · · · · u n−1<br />
u n−1 0 ... . u −1 u 0 u 1 .<br />
. . .. ... . ... . .. ... .<br />
⎜<br />
... . . .. ... . .. .<br />
⎟<br />
⎝ . . .. ... u 1−n . ... . .. u ⎠ 1<br />
u 1 u n−1 0 u 1−n · · · · · · u −1 u 0<br />
Block-partitioned LSE, cf. Rem. 2.1.4, Rem. 2.2.8<br />
⎛ ⎞⎛<br />
⎞ ⎛ ⎞<br />
u k<br />
b 1<br />
T k+1 x k+1 = ⎜ T k .<br />
⎟⎜<br />
˜x k+1<br />
( )<br />
⎟<br />
⎝ u 1 ⎠⎝<br />
⎠ = ⎜ .<br />
⎟ ˜bk+1<br />
⎝ b k<br />
⎠ = b k+1<br />
u k · · · u 1 1 x k+1 b<br />
k+1 k+1<br />
Reversing permutation: P k : {1,...,k} ↦→ {1,...,k}, P k (i) := k − i + 1<br />
˜x k+1 = T −1<br />
k (˜b k+1 − x k+1<br />
k+1 P ku k ) = x k − x k+1<br />
k+1 T−1 k P ku k ,<br />
x k+1<br />
k+1 = b k+1 − P k u k · ˜x k+1 = b k+1 − P k · x k + x k+1<br />
k+1 P k · T −1<br />
k P ku k .<br />
Efficient algorithm by using auxiliary vectors:<br />
( )<br />
x k+1 ˜x k+1<br />
=<br />
x k+1 with<br />
k+1<br />
y k := T −1<br />
k P ku k<br />
(7.5.2)<br />
(7.5.3)<br />
x k+1<br />
k+1 = (b k+1 − P k u k )/σ k<br />
˜x k+1 = x k − x k+1<br />
k+1 yk , σ k := 1 − P k u k · y k . (7.5.4)<br />
This example demonstrates the case m = n<br />
Ôº¾½ º<br />
Ôº¾¿ º<br />
In general:<br />
T = toeplitz(u(0:-1:1-m),u(0:n-1));<br />
S = toeplitz([0,u(n-1:-1:n-m+1)],[0,u(1-m:1:-1)]);<br />
( ( )<br />
x Tx<br />
C =<br />
0)<br />
Sx<br />
Computational effort O(n log n) for computing Tx (FFT based, Sect. 7.3)<br />
7.5.2 The Levinson algorithm<br />
Levinson algorithm<br />
(recursive, u n+1 not used!)<br />
Linear recursion:<br />
Computational cost ∼ (n−k) on level k, k =<br />
0, ...,n − 1<br />
➣ Asymptotic complexity O(n 2 )<br />
✄<br />
MATLAB-CODE Levinson algorithm<br />
function [x,y] = levinson(u,b)<br />
k = length(u)-1;<br />
if (k == 0)<br />
x=b(1); y = u(1); return;<br />
end<br />
[xk,yk] = levinson(u(1:k),b(1:k));<br />
sigma = 1-dot(u(1:k),yk);<br />
t= (b(k+1)-dot(u(k:-1:1),xk))/sigma;<br />
x= [ xk-t*yk(k:-1:1);t];<br />
s= (u(k+1)-dot(u(k:-1:1),yk))/sigma;<br />
y= [yk-s*yk(k:-1:1); s];<br />
Given: S.p.d. Toeplitz matrixT = (u j−i ) n i,j=1 , generating vector u = (u −n+1, ...,u n−1 ) ∈ C 2n−1<br />
(Symmetry ↔ u −k = u k , w.l.o.g u 0 = 1)<br />
Task: efficient solution algorithm for LSE Tx = b, b ∈ C n<br />
(Yule-Walker problem)<br />
Remark 7.5.3 (Fast Toeplitz solvers).<br />
FFT-based algorithms for solving Tx = b with asymptotic complexity O(n log 3 n) [37] !<br />
Supplementary and further reading:<br />
△<br />
Recursive (inductive) solution strategy:<br />
Define: T k := (u j−i ) k i,j=1 ∈ Kk,k (left upper block of T) ➣ T k is s.p.d. Toeplitz matrix ,<br />
x k ∈ K k : T k x k = (b 1 , ...,b k ) T ⇔ x k = T −1<br />
k bk ,<br />
u k := (u 1 , ...,u k ) T<br />
Ôº¾¾ º<br />
[8, Sect. 8.5]: Very detailed and elementary presentation, but the discrete Fourier transform through<br />
trigonometric interpolation, which is not covered in this chapter. Hardly addresses discrete convolution.<br />
Ôº¾ º