Numerical Methods Contents - SAM

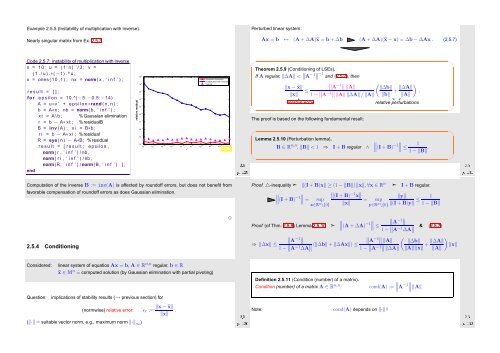
Example 2.5.5 (Instability of multiplication with inverse).
Nearly singular matrix from Ex. 2.5.3
Perturbed linear system:
Ax = b ↔ (A + ∆A)˜x = b + ∆b (A + ∆A)(˜x − x) = ∆b − ∆Ax . (2.5.7)
Code 2.5.7: instability of multiplication with inverse
1 n = 10; u = ( 1 : n ) ’ / 3 ; v =
( 1 . / u ) .∗( −1) . ^ u ;
2 x = ones ( 1 0 ,1) ; nx = norm( x , ’ i n f ’ ) ;
3
4 r e s u l t = [ ] ;
5 for e p s i l o n = 10.^(−5:−0.5:−14)
6 A = u∗v ’ + e p s i l o n∗rand ( n , n ) ;
7 b = A∗x ; nb = norm( b , ’ i n f ’ ) ;
8 x t = A \ b ; % Gaussian elimination
9 r = b − A∗ x t ; % residualB
10 B = inv (A) ; x i = B∗b ;
11 r i = b − A∗ x i ; % residual
12 R = eye ( n ) − A∗B; % residual
13 r e s u l t = [ r e s u l t ; epsilon ,
norm( r , ’ i n f ’ ) / nb ,
norm( r i , ’ i n f ’ ) / nb ,
norm(R, ’ i n f ’ ) / norm(B, ’ i n f ’ ) ] ;
14 end
relative residual
ε
Gaussian elimination
multiplication with inversel
10 0
inverse
10 −2
10 −4
10 −6
10 −8
10 −10
10 −12
10 −14
10 −16
−14 −13 −12 −11 −10 −9 −8 −7 −6 −5
10 10 10 10 10 10 10 10 10 10 Fig. 56
10 2
Ôº½¾ ¾º
✬
Theorem 2.5.9 (Conditioning of LSEs).
If A regular, ‖∆A‖ < ∥ ∥A −1∥ ∥ −1 and (2.5.7), then
∥
‖x − ˜x‖ ∥A −1∥ ∥
(
‖A‖ ‖∆b‖
≤
‖x‖ 1 − ∥ ∥A −1∥ ∥ ‖A‖ ‖∆A‖ / ‖A‖ ‖b‖ + ‖∆A‖ )
.
‖A‖
✫
relative error
The proof is based on the following fundamental result:
✬
Lemma 2.5.10 (Perturbation lemma).
✫
B ∈ R n,n , ‖B‖ < 1 ⇒ I + B regular ∧
relative perturbations
∥
∥(I + B) −1∥ ∥ ∥ ≤
1
1 − ‖B‖ .
✩
✪
✩
Ôº½¿½ ¾º
✪
Computation of the inverse B := inv(A) is affected by roundoff errors, but does not benefit from
favorable compensation of roundoff errors as does Gaussian elimination.
Proof. △-inequality ➣ ‖(I + B)x‖ ≥ (1 − ‖B‖) ‖x‖, ∀x ∈ R n ➣ I + B regular.
∥
∥(I + B) −1 x ∥ ∥
∥(I + B) −1∥ ∥ =
sup
x∈R n \{0}
‖x‖
‖y‖
= sup
y∈R n \{0} ‖(I + B)y‖ ≤ 1
1 − ‖B‖
2.5.4 Conditioning
✸
Proof (of Thm. 2.5.9) Lemma 2.5.10
⇒ ‖∆x‖ ≤
➣
∥
∥(A + ∆A) −1∥ ∥ ∥ ≤
∥ ∥ A −1∥ ∥
1 − ∥ ∥A −1 ∆A ∥ & (2.5.7)
∥
∥A −1∥ ∥
∥
1 − ∥ ∥A −1 ∆A ∥ (‖∆b‖ + ‖∆Ax‖) ≤ A −1∥ ∥ ‖A‖
1 − ∥ ∥A −1∥ ∥ ‖∆A‖
( ‖∆b‖
‖A‖ ‖x‖ + ‖∆A‖ )
‖x‖ .
‖A‖
Considered:
linear system of equatios Ax = b, A ∈ R n,n regular, b ∈ R
̂x ∈ M n ˆ= computed solution (by Gaussian elimination with partial pivoting)
Definition 2.5.11 (Condition (number) of a matrix).
Condition (number) of a matrix A ∈ R n,n ∥
: cond(A) := ∥A −1∥ ∥ ‖A‖
Question:
implications of stability results (→ previous section) for
(normwise) relative error:
(‖·‖ ˆ= suitable vector norm, e.g., maximum norm ‖·‖ ∞ )
ǫ r :=
‖x − ˜x‖
‖x‖
.
Ôº½¿¼ ¾º
Note: cond(A) depends on ‖·‖ !
Ôº½¿¾ ¾º