Einführung in die Numerische Mathematik - Lehrstuhl Numerische ...

3 Interpolation und Approximation
3.2 Spline Interpolation
Ein wesentlicher Defekt der globalen Interpolation aus dem vorherigen Abschnitt ist, dass
die interpolierenden Polynome starke Oszillationen zwischen den Stützstellen mit immer
größeren Werten annehmen. Der Grund ist die generische Steifheit, die durch die implizite
Forderung von C ∞ -Übergängen in den Stützstellen gegeben ist. Die Steifheit kann
dadurch reduziert werden, dass die globale Funktion als stückweise polynomiale (Teil)-
Funktionen bzgl. der Zerlegung a = x 0 < x 1 < . . . < x n < b zusammengesetzt wird. In
den Stützstellen x i werden dann geeignete Differenzierbarkeitseigenschaften gefordert. Am
häufigsten werden in der Literatur sogenannte kubische Splines verwendet. Allerdings hat
eine spezielle Klasse, die linearen Splines, eine besondere Bedeutung für die numerische
Lösung von Differentialgleichungen mit Hilfe der Finite Elemente Methode [10, 12].
Das wesentliche Ziel dieses Abschnitts liegt im Verständnis der stückweisen Approximation.
Dieses Konzept erlaubt die gleichmäßige Abschätzung der Konvergenz und verhindert
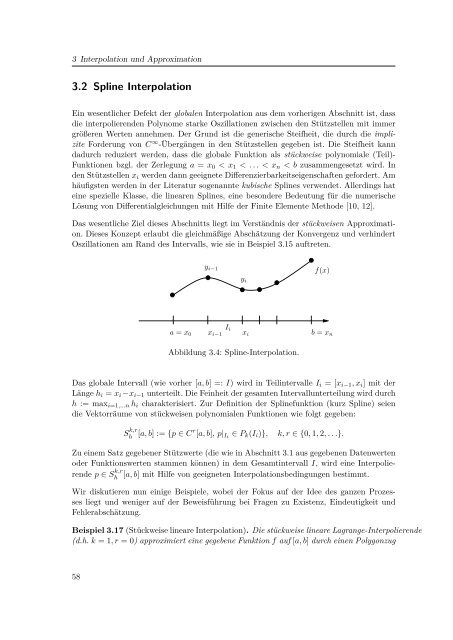
Oszillationen am Rand des Intervalls, wie sie in Beispiel 3.15 auftreten.
y i−1
y i
f(x)
I i
a = x 0 x i−1 x i b = x n
Abbildung 3.4: Spline-Interpolation.
Das globale Intervall (wie vorher [a, b] =: I) wird in Teilintervalle I i = [x i−1 , x i ] mit der
Länge h i = x i −x i−1 unterteilt. Die Feinheit der gesamten Intervallunterteilung wird durch
h := max i=1,...n h i charakterisiert. Zur Definition der Splinefunktion (kurz Spline) seien
die Vektorräume von stückweisen polynomialen Funktionen wie folgt gegeben:
S k,r
h [a, b] := {p ∈ Cr [a, b], p| Ii ∈ P k (I i )}, k, r ∈ {0, 1, 2, . . .}.
Zu einem Satz gegebener Stützwerte (die wie in Abschnitt 3.1 aus gegebenen Datenwerten
oder Funktionswerten stammen können) in dem Gesamtintervall I, wird eine Interpolierende
p ∈ S k,r
h
[a, b] mit Hilfe von geeigneten Interpolationsbedingungen bestimmt.
Wir diskutieren nun einige Beispiele, wobei der Fokus auf der Idee des ganzen Prozesses
liegt und weniger auf der Beweisführung bei Fragen zu Existenz, Eindeutigkeit und
Fehlerabschätzung.
Beispiel 3.17 (Stückweise lineare Interpolation). Die stückweise lineare Lagrange-Interpolierende
(d.h. k = 1, r = 0) approximiert eine gegebene Funktion f auf [a, b] durch einen Polygonzug
58